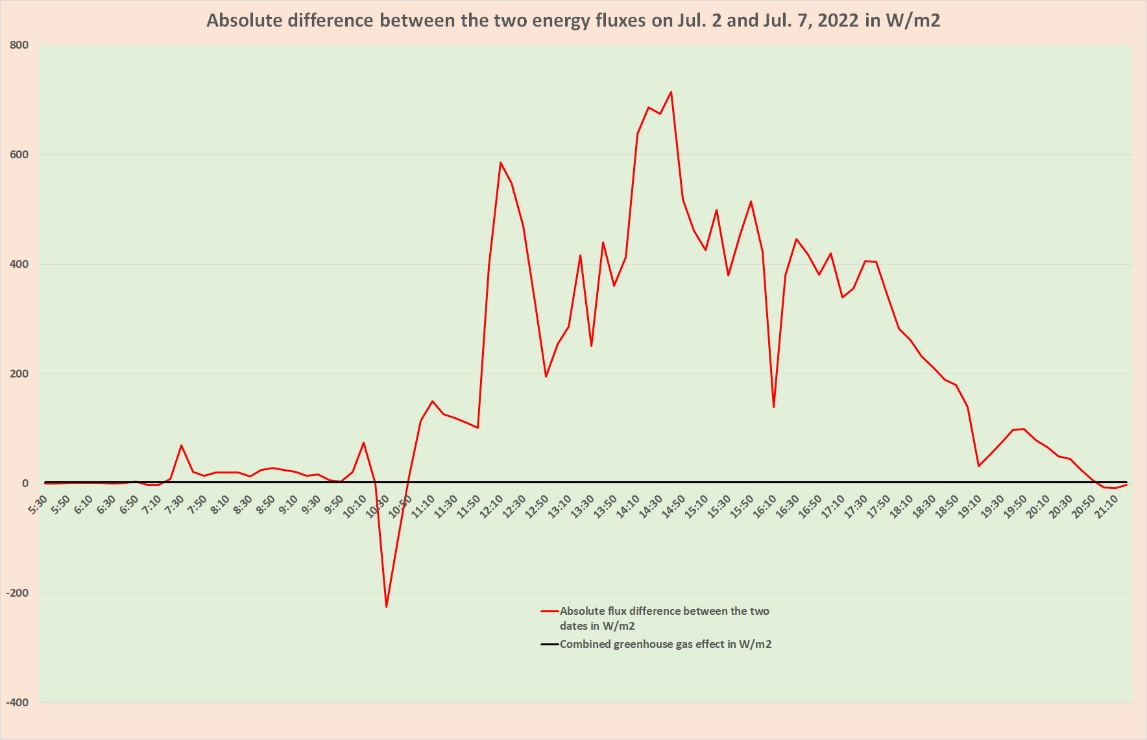
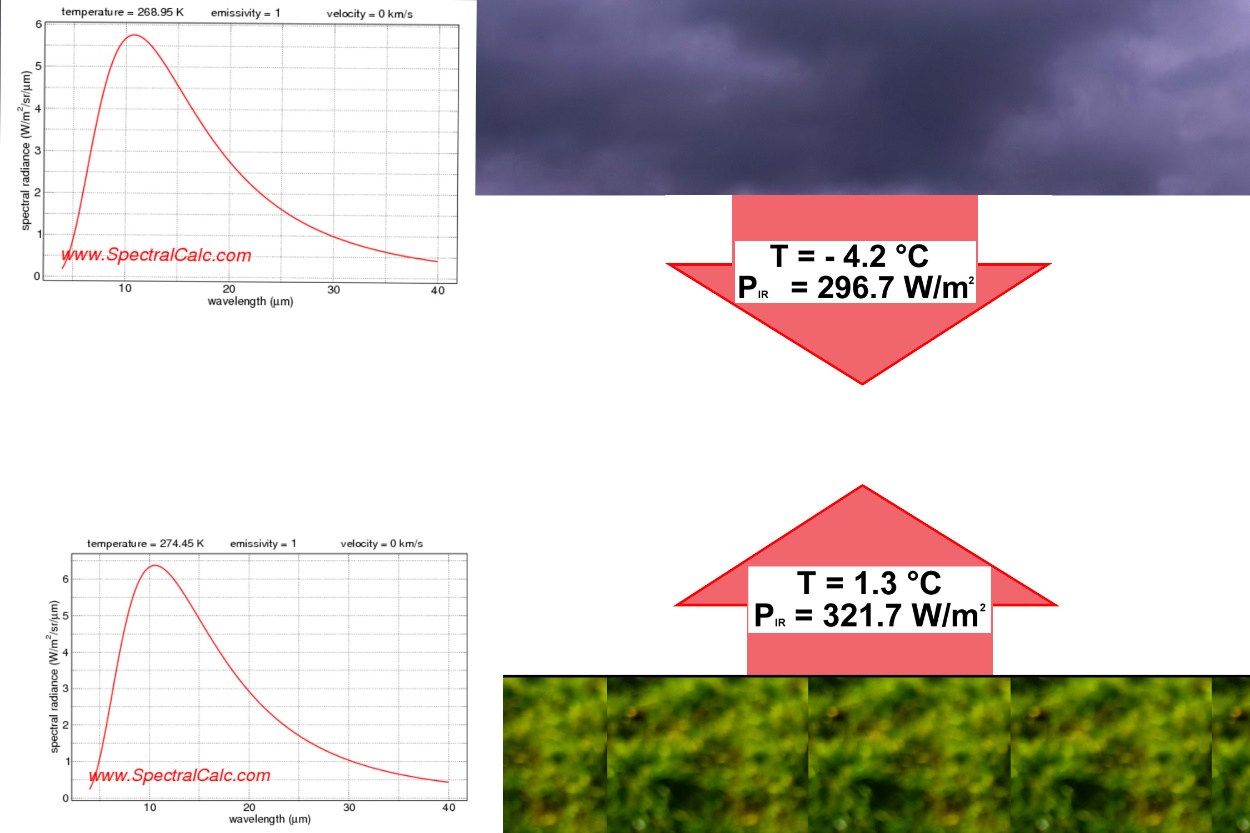
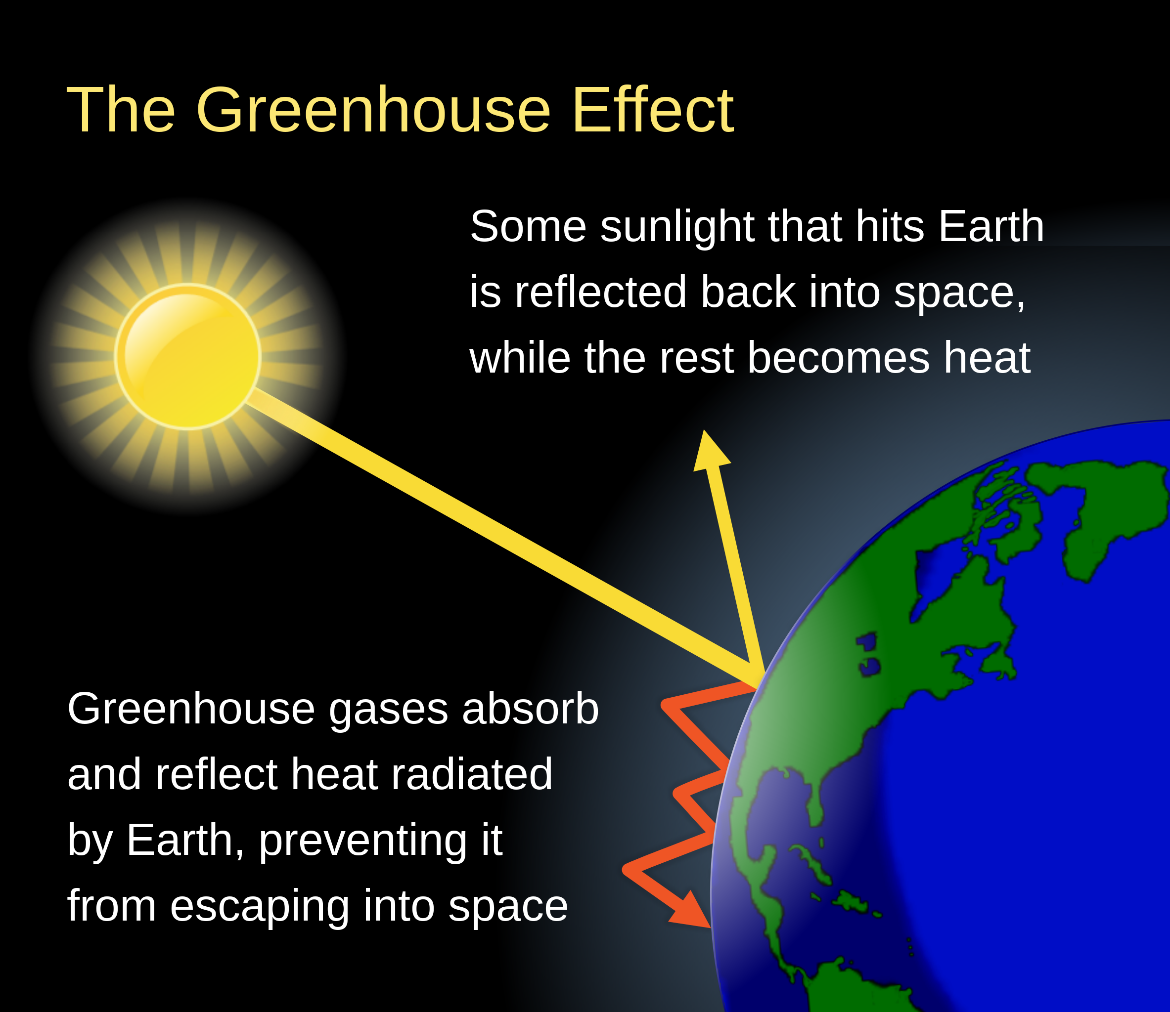
Strahlung im Treibhaus – wie oft treffen Strahlungsphotonen auf CO2 Moleküle
von Gerhard Kühn
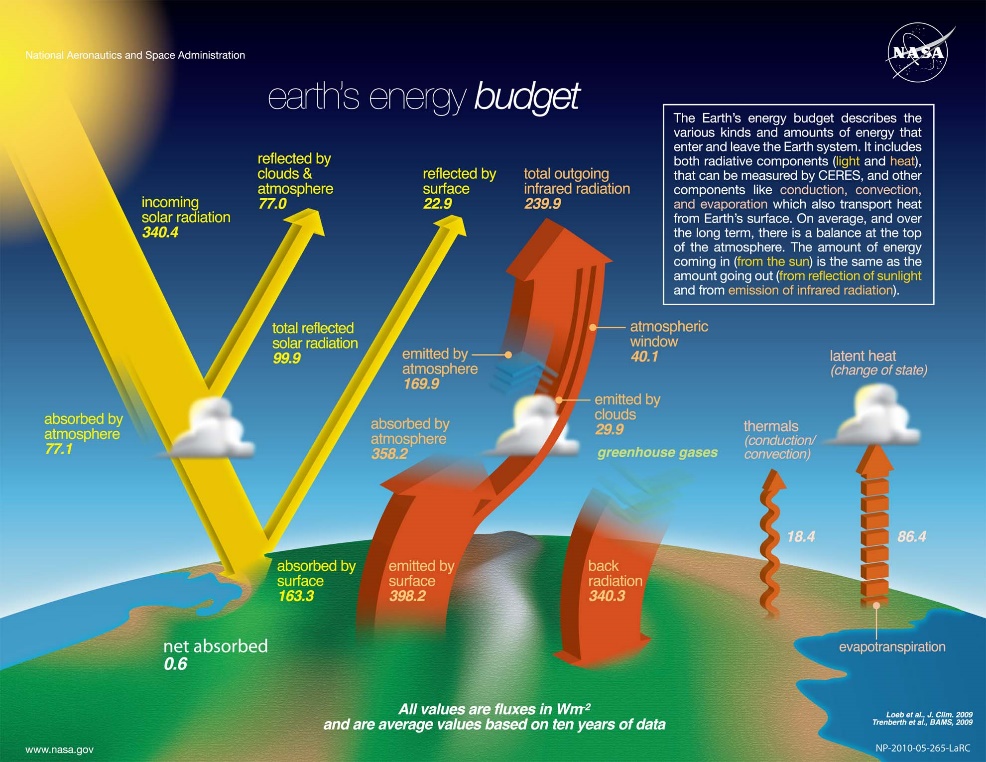
Ahnungsvoll wendet sich ein EIKE Leser Roland Hübner am 7. August 2024 an die Leser: „ vielleicht könnte auch mal ein guter Statistiker errechnen, wie wie hoch die Trefferwahrscheinkeit eines IR-Photons ist, auf ein sich in der Atmosphäre befindliches CO2 -Molekül zu treffen“. Ich habe mich von diesem Satz angesprochen gefühlt, weil ich mir oft schon die Frage gestellt habe, aus welchen Höhen die Strahlung eigentlich kommt, die angeblich dafür sorgen soll, dass aus theoretischen -18 °C angenehmere 15°C werden. Das ist letztlich die Grundidee des Treibhauseffektes. Wenn man sich die Grafiken ansieht, die den Treibhauseffekt erklären, kann man den Eindruck gewinnen, das könnten Kilometer sein, denn die Energiepfeile beginnen meistens irgendwo in der Mitte zwischen Himmel und Erde. Seltsamerweise taucht diese Fragestellung in der Klimadiskussion und -literatur weder bei Laien noch bei Fachleuten auf. Da ist manchmal die Rede von bodennaher Strahlung (Barret 13.2.25 schreibt bei EIKE von möglicherweise 100m, Ordowski von immerhin 1m),aber damit erschöpft sich auch schon das Interesse.
Ich habe die Problematik etwas modifiziert und stelle die Frage so: nach welcher Wegstrecke trifft ein IR-Photon mit 100 % iger Gewissheit spätestens auf ein CO2-Molekül und wie viele Zusammenstöße gäbe es auf seinem theoretischen Weg von der Erde durch die Atmosphäre bis ins Weltall? Dabei wird die Frage auftauchen, wie sich die Eigenbewegung der CO2 Moleküle auf die Trefferwahrscheinlichkeit auswirkt. Unter der Voraussetzung, dass die Geschwindigkeit der Photonen etwa 1 Million mal größer ist als die der CO2 -Moleküle, kann man davon ausgehen, dass ein Photon bei dieser Geschwindigkeit die CO2 -Moleküle als stillstehend „wahrnimmt“, d.h. die Eigenbewegung kann bei einer Berechnung außer Betracht bleiben.
Der folgende Lösungs-Vorschlag enthält einige gerundete Werte und Vereinfachungen, die aber letztlich an der Aussage nichts ändern. Ich habe versucht, den Vorschlag so zu formulieren, dass jeder Interessierte ihn nachvollziehen kann.
Ich gehe aus von einer Luftsäule mit einer Grundfläche von 1 cm². Der auf dieser Fläche lastende Luftdruck von ein bar ist die Folge des Wirkens von 1 kg Luft darüber mit einer angenommenen Dichte von 1,29 kg/ m ³. Das bedeutet, dass die betrachtete Luftsäule ein Volumen von 1/1,29= 0,78 m³, gleich 780 l einnimmt. Bei einer Grundfläche von 1 cm², entspricht das einer Höhe von 7,8 km, wenn man von einem konstanten Druck über die Gesamthöhe ausgeht. Diese Höhe wird in der Astronomie auch als Skalare Höhe bezeichnet. Glücklicherweise haben kluge Leute wie Avogadro und Loschmidt herausbekommen, dass 1 mol eines Gases das Volumen von 22,4 l einnimmt und dass in diesem mol 6 × 10 ^23 Moleküle enthalten sind. Das Molgewicht von CO2 beträgt 44 g. Auf der Basis diese Zahlen errechnet sich, dass sich in der Luftsäule
6•10^23 •780/22,4= 2.09•10^25 Luftmoleküle befinden. Da der Anteil des CO2 circa 423 ppm beträgt, entfallen auf das CO2 in dieser Luftsäule 8,84•10^21 CO2 Moleküle. Ein Molekül CO2 hat einen Durchmesser von 3,24•10^-10 Meter.
Zurück zur Luftsäule, die ich mir vorstelle als einen Pneumatik-Zylinder mit einem Kolben, der sich am unteren Ende der Säule, also am Boden befindet. Der Kolben soll in Gedanken eine „klebrige“ Oberfläche haben. Bewegt sich der Kolben nach oben, bleiben umso mehr CO2 Moleküle an ihm haften, je höher ich ihn anhebe. Irgendwann ist nach Zurücklegung eines Hubes h der Punkt erreicht, an dem sich auf der Oberfläche des Kolbens eine einlagige und dichte CO2 -Molekülschicht gebildet hat. diese Position ist durch die Besonderheit gekennzeichnet, dass diese Schicht für ein von unten kommendem Photon undurchdringlich ist. Das bedeutet, dass dieses spätestens nach Zurücklegen des Hubes h mit absoluter Gewissheit auf ein CO2 -Molekül treffen muss.
Jetzt ist zu ermitteln, wie viele CO2-Moleküle nötig sind, um solch eine dichte Schicht auf einer Fläche von 1 cm² (10^-4 m ²) zu bilden. Ein CO2 Molekül mit 3,24•10^-10 m Durchmesser hat eine Fläche von 8,24•10^-20 m ², das ergibt n=1,10 • 10 ^15 CO2 -Moleküle pro Schicht (die zwischen den Molekülen verbleibenden Lücken wurden mit 9 % der Fläche berücksichtigt). Ordnet man alle CO2 Moleküle der Säule in solchen Schichten an, so ergibt sich damit eine Gesamtzahl von 8•10^6 Schichten. bei einer Säulenhöhe von 7800 m ergibt sich damit schlussendlich das gesuchte Ergebnis: der Abstand der Schichten voneinander beträgt 7800 geteilt durch 8 • 10^6 = 1 mm . Irgendwie verblüffend gering. Möge sich der Leser eine eigene Meinung bilden.
Das Fazit dieser ganzen Berechnung mündet in zwei fundamentale Aussagen:
1. spätestens nach 1 mm Flug stößt das Photon mit einem CO2 Molekül zusammen.
2. auf dem Weg von der Erde bis in den Weltraum wird es 8 Millionen Mal zu einem Zusammenstoß kommen.
Das ist wahrscheinlich vielen nicht bewusst und führt zu einer Reihe von Konsequenzen.
Was passiert, wenn ein Photon mit einem CO2 Molekül zusammenstößt? Entweder wird es reflektiert oder absorbiert. Das reflektierte Photon trifft sofort wieder auf ein CO2-Molekül, und nun passiert in geometrische Folge das gleiche, kurze Zeit später sind sämtliche freiliegenden Photonen von den CO2 Molekülen eingefangen. D.h. eine Strahlung von Photonen kann sich gar nicht bilden, weil schon im status nascendi das „Leben“ der Photonen endet. D.h. auch von der Erde abfliegende Photonen dringen überhaupt nicht in die Atmosphäre ein und können demnach auch nicht aus der Atmosphäre zurückfliegen. Der gesamte Strahlen-Ansatz ist unglaubwürdig. Die Grafiken, die so etwas zeigen, entsprechen nicht der Realität.
Das Treibhaus hat also bestenfalls eine Höhe von einigen Millimetern. Was darüber ist, könnte man als Kartenhaus bezeichnen.
Es ist ja bekannt, dass auch Wasserdampf eine „Treibhaus-Wirkung“ hat, die sogar deutlich stärker ist als die von CO2. Bei einer sehr niedrig angenommene Wasserdampfkonzentration von 4000 ppm reduziert sich mit der oben angegebenen Rechenweise die freie Wegstrecke bis zum sicheren Zusammenstoß auf 0,15 mm. Rahmstorf/Schellenhuber schreiben in ihrem Buch „Der Klimawandel“ auf Seite 35:
Das wichtigste Treibhausgas Wasserdampf „taucht in der Diskussion nur deshalb nicht auf, weil der Mensch seine Konzentration nicht direkt verändern kann“.
Eine ganz eigenwillige Interpretation! In der Klimadiskussion ist auch die Rede von Substanzen, die noch stärker als CO2 wirken sollen. Bei Methan beispielsweise spricht man von 28 fachem Klimapotential. Mir ist bisher nicht klar geworden, ob dann 28 mal mehr Energie zurückgeworfen wird als ankommt. Das sieht mehr nach Perpetuum Mobile aus.
Was passiert nun mit uns und der Welt, wenn sich die derzeitige CO2 Konzentration verdoppelt? Die Antwort lautet: nahezu NICHTS. Das geht aus dem oben gesagten hervor.
Die so genannten Infrarot -sensiblen Moleküle bringen lediglich ihre eigene Masse ein. Der Molekülaufbau spielt keine Rolle. Zum analogen Ergebnis kommt man, wenn man das allgemeine Gasgesetz p•M=R•rho•T auf die Klimasituation anwendet. In einer unbeachtet gebliebenen Arbeit von Richard Kenneth „Schockstudie: Formel berechnet präzise planetarischen Temperaturen ohne Treibhauseffekt und CO2“, EIKE am 9.2.2018, wird herausgestellt, dass mit Anwendung des Gasgesetzes auf die Erde sich eine Durchschnittstemperatur von 15 °C ergibt. Nun könnte man sagen, dass die Gaskonstante sich aus den gemessenen Werten ergibt und somit 15°C herauskommen muss. Bemerkenswert ist aber, dass die Anwendung des Gasgesetzes auf die Planeten unseres Sonnensystems genau zu den Temperaturen führt, die dort gemessen worden sind. Die Abweichungen zwischen Theorie und Realität die Abweichungen zwischen Theorie und Realität sind in diesem Fall ungewöhnlich gering. Daraus ergeben sich folgende Schlussfolgerungen: Entscheidend ist für die Temperatur auf einem Planeten sind der mittlere atmosphärische Druck, die mittlere atmosphärische Dichte und die mittlere molare Masse der Atmosphäre an der Oberfläche. Die 480 °C der Venus ergeben sich auch ohne Treibhauseffekt.
Als vor circa 50 Jahren das Schwächeln der christlichen Religion immer deutlicher wurde, kamen kluge Leute zu der Erkenntnis, dass eine neue Religion nötig ist. Dazu wurde das Klima auserkoren, die Grundsätze der christlichen Religion konnten übernommen werden, genialerweise wurden aber zwei Verbesserungen eingeführt. Erstens sollten „Wissenschaftler“ mit an Bord und zweitens wurden die Frauen mit einbezogen . Als Beelzebub eignete sich das CO2, das für einen angeblich katastrophalen Temperaturanstieg verantwortlich gemacht wurde. An allem war, wie schon vorher, der Mensch Schuld.
Die Kette Schuld, Sühne, Buße, Strafe konnte nahtlos übernommen werden. Die Kirchensteuer wird heute ersetzt durch die CO2 Steuer. Der Bundestag hat neulich, ganz unauffällig und nebenbei, die rapide Erhöhung dieser Steuer beschlossen, und niemand ist sich bewusst, dass es hier um jährlich zig Milliarden geht. Professor Edenhofer wird schon oft bereut haben, dass er im Jahre 2010 folgendes gesagt hat:
„Wir (UN – IP CC) verteilen defacto den Reichtum der Welt durch die Klimapolitik… Man muss sich von der Illusion befreien, dass internationale Klimapolitik Umweltpolitik ist. Das hat fast nichts mehr mit Umweltpolitik zu tun“…[Dr. Ottmar Edenhofer, IPCC -Co-Vorsitzender der Arbeitsgruppe drei. 13. November 2010, Interview mit Doktor Charles Battig].
Aber all das hat nichts genützt, denn eine Idee wird zur materiellen Gewalt, wenn sie die Massen ergreift. Tragisch allerdings, wenn auch die Politik davon befallen ist und wirtschaftliche Auswirkungen unseren Alltag und die gesamte Wirtschaft bestimmen. Deutschland ist für globale Katastrophen mental besonders gut ansprechbar. Das Pendeln zwischen Angst (CO2) und Größenwahn (Scholz: wenn wir es nicht tun, dann tut es keiner) liegt uns besonders. Tolstoi hat das in „Krieg und Frieden“ besonders grandios vorausschauend formuliert: „nur die Deutschen sind aufgrund einer abstrakten Idee selbstbewusst, aufgrund der Wissenschaft, d.h. einer vermeintlichen Kenntnis der vollkommenen Wahrheit. Aber bei den Deutschen ist das Selbstbewusstsein schlimmer, hartnäckiger und widerwärtiger als bei allen anderen, weil er sich einbildet, die Wahrheit zu kennen, nämlich die Wissenschaft, die er sich selbst ausgedacht hat, die aber für ihn die absolute Wahrheit ist“.Seite 835ff.
Epilog: Mir ist klar, dass ich mit dem oben Gesagten irre, denn 97 % (inzwischen 99,3%) der Wissenschaftler sind, wie man so liest, anderer Meinung. Ich bitte um Aufklärung und bin dankbar und nicht beleidigt, wenn mich jemand auf meine Fehler aufmerksam macht. Ich würde es allerdings bevorzugen, wenn die Einwendungen nicht nur verbal, sondern überwiegend mit Zahlen, versehen mit den Dimensionen Länge, Masse, Zeit und Temperatur, erfolgen.
Über den Autor:
Der promovierte Ingenieur Gerhard Kühn, Jahrgang 1935, geboren Blankenburg/ Harz, Oberschule, Diplom -Ingenieur für Maschinenwesen, 1960-62 Forschungs- und Entwicklungswerk des Verkehrswesen, Blankenburg, 1963-1990 Forschungsinstitut Manfred von Ardenne, Dresden. Konstruktion, Bau und Inbetriebnahme von technischen Vakuumanlagen in der Industrie.