Chaosforscher Lorenz erneut bewiesen

geschrieben von Kip Hansen | 12. Oktober 2016

Der Höhepunkt der Presseerklärung ist das Bild rechts mit der Original-Bildunterschrift:

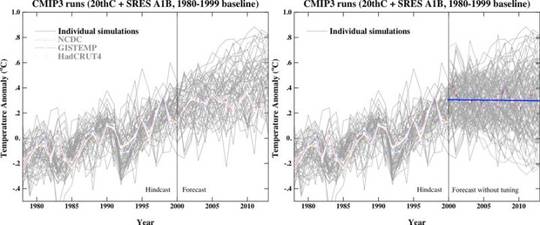
Trends der Wintertemperatur für Nordamerika zwischen 1963 und 2012 für jedes einzelne der 30 Mitglieder des CESM Large Ensemble. Die Variationen zwischen Erwärmung und Abkühlung in den 30 Membern illustrieren die weit reichenden Auswirkungen der natürlichen Variabilität, die dem vom Menschen verursachten Klimawandel überlagert sind. Das Ensemble-Mittel (EM; unten, zweites Bild von rechts) mittelt die natürliche Variabilität heraus, was allein den Erwärmungstrend zurücklässt, der dem vom Menschen verursachten Klimawandel zuzuordnen ist. Das Bild rechts unten (OBS) zeigt aktuelle Messungen aus dem gleichen Zeitraum. Vergleicht man das Ensemble Mean mit den Messungen, konnte das Wissenschaftlerteam aufgliedern, ein wie großer Anteil an der Erwärmung in Nordamerika der natürlichen Variabilität und welcher Anteil dem vom Menschen verursachten Klimawandel geschuldet ist. Die ganze Studie steht im American Meteorological Society’s Journal of Climate. (© 2016 AMS.)

Was ist das? Das Large Ensemble Community Project des UCAR hat eine Datengrundlage erzeugt von „30 Simulationen mit dem Community Earth System Model (CESM) mit einer Auflösung von 1° Länge/Breite. Jede einzelne Simulation erfährt ein identisches Szenario historischen Strahlungsantriebs, startet jedoch jeweils von einem etwas unterschiedlichen atmosphärischen Zustand“. Aber genau welche Art von „unterschiedlicher atmosphärischer Zustand“ ist gemeint? Wie unterschiedlich waren die Anfangsbedingungen? „Die Wissenschaftler modifizierten die Anfangsbedingungen des Modells leicht, indem sie die globale atmosphärische Temperatur um weniger als ein Billionstel Grad variierten“.

Die Bilder, Nummern 1 bis 30, repräsentieren jeweils die Ergebnisse eines Einzellaufes des CESM mit einheitlichen, sich um ein Billionstel Grad unterscheidenden Anfangstemperatur – jede einzelne eine Projektion der Wintertemperaturtrends in Nordamerika im Zeitraum 1963 bis 2012. Das Bild rechts unten mit der Bezeichnung OBS zeigt die tatsächlich beobachteten Trends.

Es gibt eine Studie, aus der dieses Bild stammt: Forced and Internal Components of Winter Air Temperature Trends over North America during the past 50 Years: Mechanisms and Implications. Dabei handelt es sich um eine Studie, die lediglich eine von „etwa 100 begutachteten Artikeln in wissenschaftlichen Journalen ist, welche Daten des CESM Large Ensemble herangezogen hatten“. Ich werde diese Studie nicht kommentieren, sehr wohl aber das Bild, dessen Bildunterschrift sowie die Statements in der Presseerklärung selbst.

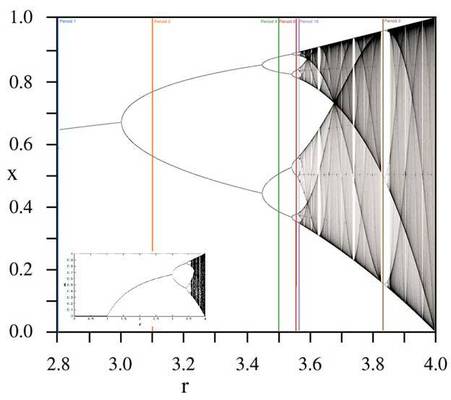
Ich bekenne verblüfft zu sein – nicht durch die Tatsache, dass 30 CESM-Modellläufe 30 vollkommen unterschiedliche 50-Jahre-Klimaprojektionen aus nahezu identischen Ausgangsbedingungen erzeugt haben. Das war absolut zu erwarten. Tatsächlich zeigte dies schon Edward Lorenz mit seinen Spielzeug-Wettermodellen auf seinem (verglichen mit heutigen Standards) „Spielzeug“-Computer in den sechziger Jahren. Seine Entdeckungen führten zu einem Studienbereich, der heute als Chaos-Theorie bekannt ist, also die Untersuchung nichtlinearer dynamischer Systeme, vor allem solcher, die hoch sensitiv bzgl. ihrer Ausgangsbedingungen sind. Unsere 30 CESM-Läufe wurden initialisiert mit einem Unterschied von – was? Ein Billionstel Grad beim Anfangswert der globalen atmosphärischen Temperatur – ein so geringer Betrag, dass er buchstäblich von modernen Thermometern unmessbar ist. Lässt man die Simulationen gerade mal über 50 Jahre laufen – von 1963 bis 2012 – ergeben sich Resultate vollständig den Ergebnissen von Lorenz zufolge: „Zwei Zustände, die sich nicht wahrnehmbar unterscheiden, können bei der Simulation eventuell zwei Zustände herauskommen, die sich erkennbar unterscheiden … Falls es dann zu irgendeinem Fehler welcher Art auch immer kommt bei der Messung des Ist-Zustandes – und in jedwedem realen System sind derartige Fehler unvermeidlich – kann eine akzeptable Vorhersage eines unmittelbaren Zustandes in ferner Zukunft sehr gut unmöglich sein … Angesichts der unvermeidlichen Ungenauigkeit und der Unvollständigkeit von Wetterbeobachtungen wären präzise langfristige Vorhersagen nicht existent“.

Worin liegt die Bedeutung von Lorenz? Von buchstäblich ALLEN unserer Daten der historischen „globalen atmosphärischen Temperatur“ weiß man, dass sie um mindestens ±0,1°C ungenau sind. Egal welcher Initialwert die engagierten Leute am NCAR/UCAR in das CESM als globale atmosphärische Temperatur eingeben, es wird sich von der Realität um viel, viel mehr Größenordnungen unterscheiden als der Temperaturunterschied von 1 Billionstel Grad bei der Initialisierung dieser 30 CESM-Läufe ausmacht. Spielt das wirklich eine Rolle? Meiner Ansicht nach spielt es keine Rolle. Man kann leicht erkennen, dass die kleinsten aller Unterschiede, selbst bei einem einzelnen Initialwert, zu 50-Jahre-Projektionen führen, die sich so stark voneinander unterscheiden wie nur irgend möglich (siehe Fußnote 1 unten). Ich weiß nicht, wie viele Initialbedingungen in das CESM eingehen müssen, um es zu initialisieren – aber es ist sicher mehr als nur eine. Um wieviel mehr würden sich die Projektionen unterscheiden, falls jeder der Initialwerte verändert werden würde, selbst wenn auch nur leicht?

Was mich verblüfft ist die in der Bildunterschrift enthaltene Behauptung: „Das Ensemble-Mittel (EM; unten, zweites Bild von rechts) mittelt die natürliche Variabilität heraus, was allein den Erwärmungstrend zurücklässt, der dem vom Menschen verursachten Klimawandel zuzuordnen ist“.

In der Studie, die zur Erstellung dieser Graphik geführt hat, lautet die präzise Behauptung:

Dieser Rahmen der Modellierung enthält 30 Simulationen des Community Earth System Model (CESM) mit einer Auflösung von 1° Länge/Breite, von denen jede Einzelne ein identisches Szenario des historischen Strahlungsantriebs erfährt, aber mit einem leicht unterschiedlichen atmosphärischen Anfangszustand. Folglich resultiert jedweder Spread innerhalb der Ensemble-Ergebnisse aus der unvorhersagbaren internen Variabilität, die sich dem erzwungenen Klimawandel-Signal überlagert.

Dieser Gedanke ist sehr verführerisch. Oh wie schön es wäre, wenn das stimmen würde – falls es wirklich so einfach wäre.

Aber so einfach ist es nicht. Und meiner Überzeugung nach ist er fast mit Sicherheit falsch.

Das Klimasystem ist ein gekoppeltes, nichtlineares und chaotisches dynamisches System – wobei die beiden gekoppelten Hauptsysteme die Atmosphäre einerseits und die Ozeane andererseits sind. Diese beiden sich ungleich erwärmenden Systeme agieren unter dem Einfluss der Gravitationskräfte von Erde, Mond und Sonne, während sich der Planet im All dreht und einem ungleichmäßigen Orbit um die Sonne folgt. Dies erzeugt ein kombiniertes dynamisches System unglaublicher Komplexität, welches die erwarteten Typen chaotischer Phänomene zeigt, die von der Chaos-Theorie vorhergesagt werden – wobei ein Aspekt dieser Theorie eine ausgeprägte Abhängigkeit von den Anfangsbedingungen ist. Wenn ein solches System mathematisch modelliert wird, ist es unmöglich, alle Nichtlinearitäten zu eliminieren (vielmehr ist es so, dass ein Modell umso ungültiger ist, je mehr die nichtlinearen Formeln vereinfacht werden).

Die Mittelung von 30 Ergebnissen, die durch das mathematisch chaotische Verhalten jedweden dynamischen Systems erzeugt werden, „mittelt die natürliche Variabilität NICHT heraus“ in dem modellierten System. Die Mittelung bringt nicht einmal auch nur ansatzweise Derartiges zustande. Die Mittelung von 30 chaotischen Ergebnissen erzeugt lediglich das „Mittel jener speziellen 30 chaotischen Ergebnisse“.

Warum wird mit der Mittelung die natürliche Variabilität herausgemittelt? Weil es einen gewaltigen Unterschied gibt zwischen Zufalls-Systemen und chaotischen Systemen. Diesen Unterschied scheint man bei der Aufstellung der obigen Behauptung übersehen zu haben.

Das Werfen einer Münze (mit einer nicht gezinkten Münze) ergibt Zufallsergebnisse – nicht Kopf-Zahl-Kopf-Zahl. Wenn man die Münze oft genug geworfen hat, ist es möglich, die Zufälligkeit herauszumitteln und zu einem wahren Verhältnis möglicher Ergebnisse zu kommen – welches 50 zu 50 für Kopf-Zahl sein wird.

[Anders gesagt: Hier wird der in der Tat gravierende Unterschied angesprochen zwischen deterministischem Chaos {Klima, Wetter} und dem absoluten Chaos {Würfel, Münzwurf}. Anm. d. Übers.]

Dies gilt nicht für chaotische Systeme. In chaotischen Systemen scheinen die Ergebnisse nur zufällig zu sein – aber sie sind in keiner Weise zufällig – sie sind durchweg deterministisch, wobei jeder nachfolgende Zustand präzise bestimmt wird durch die Anwendung einer speziellen Formel auf den bestehenden Wert, was man dann bei dem folgenden Wert wiederholt. Bei jedem Wechsel kann der nächste Wert exakt berechnet werden. Was man in einem chaotischen System nicht tun kann, ist vorherzusagen, welcher Wert nach den nächsten 20 Wechseln auftreten wird. Man muss sich durch jeden einzelnen der 19 Schritte zuvor hindurch rechnen, um dorthin zu kommen.

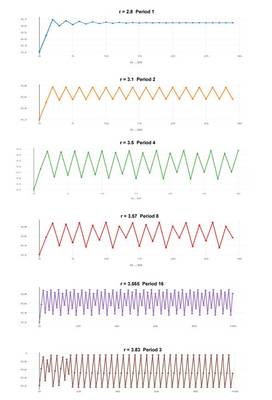
In chaotischen Systemen haben diese Nicht-Zufalls-Ergebnisse – obwohl sie zufällig aussehen können – Ordnung und Struktur. Jedes chaotische System weist Regimes der Stabilität, Periodizität, Perioden-Verdoppelung auf, welche nach Zufall aussehen, aber im Wert abhängig sind. In einigen Fällen treten auch Regimes auf, die hoch geordnet in etwas sind, was man „Fremd-Attraktoren“ [strange attractors] nennt. Einige dieser Zustände, dieser Regimes, sind Gegenstand statistischer Analysen und können als „glatt“ [smooth] angesehen werden (Regionen, die statistisch gleichmäßig daherkommen) – andere variieren phantastisch, wunderschön anzusehen im Phasenraum [phase space], und ausgeprägt „un-glatt“ [un-smooth], wobei einige Regionen vor Aktivität strotzen, während andere kaum angesprochen werden und die zutiefst widerstandsfähig sind gegen einfache statistische Analyse – obwohl es ein Studienbereich in der Statistik gibt, der sich auf dieses Problem konzentriert. Dies involviert jedoch nicht die Art des Mittels, das in diesem Falle herangezogen wird.

Die Ergebnisse chaotischer Systeme können folglich nicht einfach gemittelt werden, um Zufälligkeit oder Variabilität herauszumitteln – die Ergebnisse sind nicht zufällig und nicht notwendigerweise gleich variabel. In unserem Fall haben wir absolut keine Ahnung bzgl. Gleichheit und Glätte des realen Klimasystems.

Auf einem grundlegenderen Niveau wäre die Mittelung von 30 Ergebnissen nicht einmal gültig für ein echt zufälliges Zwei-Werte-System wie dem Werfen einer Münze oder ein Sechs-Werte-System beim Werfen eines einzigen Würfels. Dies ist für jeden Statistik-Student im ersten Semester offensichtlich. Vielleicht ist es die nahezu unendliche Anzahl möglicher chaotischer Ergebnisse des Klimamodells, welche es so aussehen lässt, als ob ein gleichmäßiger Spread von Zufallsergebnissen vorliegt, der es dem Anfänger erlaubt, diese Regel zu ignorieren.

Hätten sie das Modell 30 oder 100 mal mehr laufen lassen und unterschiedliche Ausgangsbedingungen adjustiert, würden sie potentiell einen vollkommen unterschiedlichen Satz von Ergebnissen bekommen – vielleicht eine Kleine Eiszeit in einigen Läufen – und sie hätten ein unterschiedliches Mittel. Würde man von diesem neuen, unterschiedlichen Mittel auch sagen, dass es ein Ergebnis repräsentiert, welches „die natürliche Variabilität herausmittelt, was allein den Erwärmungstrend zurücklässt, der dem vom Menschen verursachten Klimawandel zuzuordnen ist“? Wie viele unterschiedliche Mittelwerte könnten auf diese Art und Weise erzeugt werden? Ich habe den Verdacht, dass sie nichts anderes repräsentieren würden als das Mittel aller möglichen Klima-Outputs dieses Modells.

Das Modell hat von Anfang an nicht wirklich irgendeine „natürliche Variabilität“ – es gibt keine Formel in dem Modell, von der man sagen kann, dass sie jenen Part des Klimasystems repräsentiert, der „natürliche Variabilität“ ist – was das Modell hat, sind mathematische Formeln, die vereinfachte Versionen der nichtlinearen mathematischen Formeln sind, die Dinge repräsentieren wie den Nicht-Gleichgewichts-Wärmetransfer [non-equilibrium heat transfer], den dynamischen Fluss ungleichmäßig erwärmter Flussobjekte, konvektive Abkühlung, Flüsse aller Arten (Ozeane und Atmosphäre), von deren Dynamik man weiß, dass sie in der realen Welt chaotisch sind. Die mathematisch chaotischen Ergebnisse spiegeln das, was wir als „natürliche Variabilität“ kennen – wobei dieser Terminus nur Gründe nichtmenschlicher Natur meint – und sind in das Modell als solches eingebaut. Die chaotischen Klima-Ergebnisse der realen Welt, welche die wahre natürliche Variation sind, verdanken ihre Existenz den gleichen Prinzipien – der Nichtlinearität dynamischer Systeme – aber die in der realen Welt agierenden dynamischen Systeme, in denen die natürliche Variabilität nicht nur jene in das Modell eingebaute „Natürlichkeit“ enthält, sondern auch alle jene Ursachen, die wir nicht verstehen, sowie jene, die uns nicht bewusst sind. Es wäre ein Fehler, die beiden unterschiedlichen Variabilitäten als eine Identität anzusehen – ein und dasselbe.

Folglich kann man nicht sagen, dass „jedweder Spread im Ensemble“ die Folge der internen Variabilität des Klimasystems ist oder jenen als buchstäblich die „natürliche Variabilität“ repräsentierend ansehen, und zwar in dem Sinne, in dem dies in der Klimawissenschaft allgemein genannt wird. Der Spread im Ensemble resultiert einfach aus dem mathematischen Chaos, das inhärent in den Formeln steckt, die im Klimamodell gerechnet werden. Er repräsentiert lediglich den Spread, den erzwungene Struktur und die Parametrisierung des Modells selbst.

Man erinnere sich, jedes der 30 Bilder aus den 30 Modellläufen des CESM sind durch einen identischen Code erzeugt worden, identische Parameter, identische Antriebe – aber unter alles andere als identischen Ausgangsbedingungen. Und doch passt keines der Ergebnisse zum beobachteten Klima des Jahres 2012. Nur eines kommt diesem halbwegs nahe. Niemand glaubt, dass diese tatsächliche Klimazustände repräsentieren. Ein volles Drittel der Läufe erzeugt Projektionen, die wenn sie für 2012 passend gewesen wären, die Klimawissenschaft auf den Kopf gestellt hätten. Wie können wir dann annehmen, dass die Mittelung dieser 30 Klimazustände auf magische Weise irgendwie das reale Klima repräsentieren kann mit der herausgemittelten natürlichen Variabilität? Dies sagt uns in Wirklichkeit nur, wie ausgesprochen empfindlich das CESM gegenüber den Ausgangsbedingungen ist. Und es sagt uns etwas über die Grenzen projizierter Klimazustände, die das modellierte System zulassen kann. Was wir im Ensemble-Mittel und Spread sehen, ist lediglich das Mittel jener exakten Läufe und deren Spread über einen 50-jährigen Zeitraum. Aber es hat kaum etwas zu tun mit dem realen Weltklima.

Die mathematisch chaotischen Ergebnisse des modellierten dynamischen Systems mit der „natürlichen Variabilität“ der realen Welt – die Behauptung, dass beides ein und dasselbe ist – ist eine Hypothese ohne Grundlage, vor allem dann, wenn man die Klimaauswirkungen in ein Zwei-Werte-System aufteilt, das einzig die „natürliche Variabilität“ und den „vom Menschen verursachten Klimawandel“ enthält.

Die Hypothese, dass die Mittelung von 30 chaotisch erzeugten Klimaprojektionen ein Ensemble Mean erzeugt, folgt mit Sicherheit nicht aus einem Verständnis der Chaos-Theorie. Zumindest wenn dieses Ensemble Mean die natürliche Variabilität auf eine Art und Weise herausgemittelt hat, dass der Vergleich der EM-Projektion mit den tatsächlich gemessenen Daten erlaubt „zu zergliedern, wie viel der Erwärmung in Nordamerika der natürlichen Variabilität und wie viel davon dem vom Menschen verursachten Klimawandel“ geschuldet ist.

Das Zwei-Werte-System (natürliche Variabilität vs. vom Menschen verursacht) ist nicht ausreichend. Weil wir keine adäquaten Kenntnisse darüber haben, welche alle diese natürlichen Gründe sind (auch nicht über die wahre Größenordnung ihrer Auswirkungen), können wir sie nicht von all den menschlichen Gründen trennen – wir können noch nicht Ausmaße von Auswirkungen abgrenzen wegen der „natürlichen“ Gründe, und folglich können wir auch nicht den „vom Menschen verursachten Rest“ berechnen. Wie auch immer, vergleicht man das Ensemble Mean vieler nahezu identischer Läufe eines modellierten, bekannt chaotischen Systems mit den Beobachtungen der realen Welt, ist dies kein mathematisch oder wissenschaftlich gestütztes Verfahren im Lichte der Chaos-Theorie.

Im Klima-System gibt es bekannte Ursachen, und es verbleibt die Möglichkeit unbekannter Ursachen. Der Vollständigkeit halber sollten wir bekannte Unbekannte erwähnen – wie etwa Wolken sowohl Auswirkung als auch Ursache sind. In unbekannten Beziehungen – und unbekannten Unbekannten – mag es Ursachen für klimatische Änderungen geben, die uns bislang nicht einmal andeutungsweise bekannt sind, obwohl die Möglichkeit bedeutsamer „Großer-Roter-Knopf“-Ursachen des verbleibenden Unbekannten von Jahr zu Jahr abnehmen. Und doch, weil das Klimasystem ein gekoppeltes, nichtlineares System ist – chaotisch in seiner ureigenen Natur – ist das Auseinanderfieseln der gekoppelten Ursachen und Auswirkungen ein laufendes Projekt und wird es auch noch lange bleiben.

Man beachte auch, dass weil das Klimasystem seiner Natur nach ein eingezwängtes [constrained] chaotisches System ist (siehe Anmerkung 2), wie diese Studie zu zeigen versucht, kann es einige Klima-Ursachen geben, welche – obwohl sie so klein sind wie „eine Änderung der globalen atmosphärischen Temperatur um ein Billionstel Grad“ – zukünftig Klimaänderungen auslösen können, die viel, viel größer sind als wir uns vorstellen können.

Was das vom NCAR/UCAR Large Ensemble Community Project erzeugte Image tatsächlich bewirkt, ist die totale Validierung der Entdeckung von Edward Lorenz, dass Modelle von Wetter- und Klimasystemen ihrer ureigenen Natur nach chaotisch sind und unabdingbar sein müssen – ausgesprochen empfindlich gegenüber Anfangsbedingungen – und sich daher Versuchen einer „präzisen Langfristvorhersage“ entziehen.

——————————————————-

Anmerkungen:

1. Klimamodelle sind so parametrisiert, das sie erwartete Ergebnisse erzeugen. Beispiel: Falls ein Modell allgemein keine Ergebnisse erzeugen kann, die aktuelle Beobachtungen spiegeln, wenn man sie zur Projektion bekannter Daten heranzieht, dann muss es solange adjustiert werden, bis das doch der Fall ist. Es ist offensichtlich: falls ein Modelllauf im Jahre 1900 startet und über 100 Jahre projiziert und sich dabei eine Kleine Eiszeit bis zum Jahr 2000 ergibt, dann muss man davon ausgehen, dass irgendetwas in dem Modell fehlt. Dieser Gedanke ist berechtigt, obwohl es zunehmende Beweise gibt, dass die spezifische Praxis ein Faktor sein kann für die Unfähigkeit der Modelle, selbst kurzfristige Zukunft (Dekaden) korrekt zu projizieren, und für deren unverändertes Erzeugen von Erwärmungsraten weit oberhalb der gemessenen Raten.

2. Ich beziehe mich auf das Klimasystem als „eingezwängt“ allein auf der Grundlage unseres langfristigen Verständnisses des Klimas der Erde – Temperaturen verharren in einem relativ engen Band, und größere Klimazustände scheinen auf Eiszeiten und Zwischeneiszeiten beschränkt zu sein. Genauso in der Chaos-Theorie – Systeme sind bekannt eingezwängt durch Faktoren innerhalb des Systems selbst – obwohl sich die Ergebnisse als chaotisch erweisen können, sind sie nicht „bloß irgendetwas“, sondern ereignen sich innerhalb definierter mathematischer Räume – von denen einige phantastisch kompliziert sind.

Link: https://judithcurry.com/2016/10/05/lorenz-validated/

Übersetzt von Chris Frey EIKE



Chaos & Klima – Teil 3: Chaos & Modelle

geschrieben von Kip Hansen | 12. Oktober 2016

In diesem Essay geht es darum, die möglichen Verbindungen zwischen Klima und Chaos zu klären. Dies ist keine hochtechnische Diskussion, sondern eine grundlegende Einführung zu diesem Thema, um etwas zu erhellen, was das IPCC meint mit seiner Aussage „wir haben es mit einem gekoppelten, nichtlinearen und chaotischen System“ zu tun und wie dies unser Verständnis von Klima und Klimawissenschaft verändern könnte. Dies ist der Dritte Teil einer Reihe. Die anderen beiden Teile stehen hier (Teil 1) und hier (Teil 2). In diesem Beitrag geht es um Periodenverdoppelung, welche zu Chaos führt, und darum, was Chaos für die Klimamodellierung bedeutet.

Es ist wichtig, nicht zu vergessen, dass jedwede Verwendung des Wortes Chaos (und dessen Ableitung chaotisch) in diesem Essay die Absicht hat, Bedeutungen zu haben im Sinne der Chaos-Theorie, „also der Bereich in der Mathematik, der das Verhalten dynamischer Systeme zum Inhalt hat, die hoch sensitiv sind gegenüber den Ausgangsbedingungen“. Das Wort Chaos bedeutet hier nicht „vollständige Konfusion und Unordnung: ein Zustand, in dem Verhalten und Ereignisse durch nichts kontrolliert werden“. Vielmehr bezieht es sich hier auf dynamische Systeme, in denen „kleine Differenzen in den Ausgangsbedingungen … erheblich voneinander abweichende Ergebnisse zeitigen … mit dem Beweis, dass langfristige Prophezeiungen allgemein unmöglich sind. Dies ist sogar in deterministischen Systemen der Fall. Dies bedeutet, dass deren zukünftiges Verhalten vollständig von den Ausgangsbedingungen bestimmt wird, ohne Einbeziehung irgendwelcher zufälliger Elemente. Mit anderen Worten, die deterministische Natur dieser Systeme macht sie nicht [automatisch] vorhersagbar. Edward Lorenz nannte dies ein „scheinbar zufälliges und unvorhersagbares Verhalten, das nichtsdestotrotz präzisen und oftmals einfach zu beschreibenden Regeln folgt“. Falls man diesen wichtigen Unterschied nicht versteht, wird man das gesamte Thema völlig missverstehen. Falls Obiges nicht klar ist (was keine Überraschung wäre, ist dies doch kein einfaches Konzept), lese man zumindest den Beitrag bei Wikipedia zur Chaos-Theorie.

Das Problem der Periodenverdoppelung

Die klassische mathematische Formel, die die Prinzipien der Chaos-Theorie beschreibt, ist die logistische Gleichung, die ich in dieser Beitragsreihe immer wieder verwendet habe.

Der Biologe Robert May gebraucht sie als ein „demographisches Modell analog der logistischen Gleichung“ … wobei „xn eine Zahl zwischen Null und Eins ist, die das Verhältnis der bestehenden Bevölkerung zur maximal möglichen Bevölkerung repräsentiert“. Der Parameter r ist die reproduktive Rate, ausgedrückt in ganzen Zahlen. In der logistischen Karte konzentrieren wir uns auf das Intervall (0, 4). Wenn wir das tun, erzeugt es das universelle Bifurkations-Diagramm für die logistische Gleichung, oder logistische Karte, welche die Charakteristiken zeigt, wenn sich der Parameter r ändert:

Dem folgen Zeitreihen der Ergebnisse bei verschiedenen Werten von r – was mit den farbigen vertikalen Linien korrespondiert:

Für jetzt wollen wir die Bereiche ignorieren, die nahezu durchgehend mit grau bedeckt sind und uns auf die Schnittpunkte mit den farbigen Linien konzentrieren. Wir sehen, dass die Zunahme von r bis 3,1 eine Sägezahn-Graphik erzeugt mit einer Periode von 2. Bei 3,5 verdoppelt sich die Periode auf 4, dann rapide auf 8 und dann 16 (es gibt auch Punkte für 32 und 64 usw.). Außerdem reichen die Magnituden-Werte (die x) von einer engen Bandbreite von 20% der Einheit bei der Periode 2 bis zu kolossalen 45% der Einheit (die gesamte Bandbreite) bei Periode 4.

Falls wir die Dynamik des Windes über dem neuen Design einer Flugzeug-Tragfläche betrachten, würden wir als Erstes eine kleine unerklärliche Vibration erkennen (da der Wert unseres r kaum über 3 hinausgeht), gefolgt von einem definitiven Schütteln bei r = 3,1. Dann beobachte man, wie sich das Ding sich selbst in Stücke zerlegt, wenn r immer weiter zunimmt.

Einige könnten denken, dass dies irgendwie eine „Rückkopplung“, ein „Rückkopplungs-Loop“ oder ein „Runaway-Rückkopplungs-Loop“ ist. Sie hätten unrecht. Das Ergebnis – unsere sich selbst in Stücke zerlegende arme hypothetische Flugzeug-Tragfläche – sieht sicher so ähnlich aus, aber die Ursache ist eine ganz andere. Dies ist ein universelles Phänomen chaotischer, nichtlinearer Systeme, repräsentiert durch das Bifurkations-Diagramm. In gewisser Weise gibt es keine andere Ursache als die Natur des Systems selbst.

Man vergesse nicht, es muss einen Grund geben für die Zunahme des Faktors r – aber eine Zunahme von r – sagen wir mal eine Verdoppelung von 1 auf 2 – führt weder zu Instabilität noch zu Chaos, sondern nur zu einer Zunahme der Magnitude von x (siehe das kleine eingefügte Bild im größeren Bild oben). Die Zunahme von r von 2 auf 2,5 hat den gleichen harmlosen Effekt, nämlich eine Zunahme der Magnitude von x. Die einfache Tatsache des Zunehmenden r führt nicht zu einer Verdoppelung der Periode selbst – sondern, wie ich in Teil 2 dieser Reihe gezeigt habe, zu Stabilität bei höheren Werten von x – es sei denn, der Wert von r wird größer als 3. An diesem Punkt beginnt der Prozess der Perioden-Verdoppelung, was zu Chaos führt.

(Es gibt viele nicht lineare, chaotische Systeme in der physikalischen Welt, die alle ihre eigenen Parameter und Formeln haben, und die ihre eigenen Bedingungen haben, an welchen in dem System die Perioden-Verdoppelung und damit das Chaos beginnt. Lediglich in der logistischen Gleichung ist die magische Zahl 3).

Man beachte auch die anderen ziemlich komischen Dinge hier: bei 3,8+ gibt es ein Fenster mit einer Periode 3, welches in eine Periode 6 springt, dann 12, dann 24 … die kleine Bifurkation nahe dem untersten Teil der braunen Linie bei 3,8 sieht – falls man sie vergrößert – genau so aus wie eine invertierte Version des gesamten Diagramms – ein Vorgang, dem man Selbst-Ähnlichkeit nennt, den wir aber hier nicht behandeln.

Gibt es das auch in der realen Welt? Jawohl! Boomende und vergehende Tierpopulationen, Wirtschaft (siehe eine logistische Karten für eine modifizierte Phillips-Kurve hier), in strömenden Flüssigkeiten, in den Vibrationen von Systemen in Bewegung, in unregelmäßigen Herztönen, was zu lebensbedrohenden Bedingungen führt. Sprünge der Perioden-Verdoppelung sind allgemein und können in physikalischen Systemen ziemlich destruktiv sein.

Diese Art von Phänomenen kann die Ursache sein für den Zusammenbruch der Tacoma Narrows-Brücke (1940) hier, von dem es bei Wiki heißt: „In vielen Physik-Lehrbüchern wird dieses Ereignis als ein Musterbeispiel für elementar erzwungene Resonanz angeführt, wobei der Wind eine externe periodische Frequenz zeigt, die zu der natürlich strukturierten Frequenz der Brücke passte, obwohl der tatsächliche Grund für den Zusammenbruch aeroelastisches Flattern [aeroelastic flutter] war“. Man beachte, dass der Wind nur mit etwa 40 mph [ca. 64 km/h bzw. 6 Bft] wehte.

Herzspezialisten haben mit der Chaos-Theorie gearbeitet sowie mit der ins Chaos führenden Perioden-Verdoppelung bei der Untersuchung von Herzschlag-Unregelmäßigkeiten wie etwa cardiac dysrhythmias, ventricular fibrillation and pulseless ventricular tachycardia. Hier folgt ein Ausschnitt aus meinem letzten EKG, welcher die elektrischen Impulse zeigt, wenn mein Herz vier mal schlägt:

Man versicherte mir, dass es genauso aussieht wie es aussehen muss. Allerdings kann es auch schief laufen, und das passiert auch tatsächlich:

Der Schnelle Herzschlag oben (Herzrasen) scheint eine Verdoppelung des Herzschlags zu sein. Shannon Lin an der UC Davis, berichtet in einer Studie mit dem Titel „Chaos in Human Systems”, dass im Falle von Herzrhytmus-Störungen EKGs implementiert werden, um die vom Herz erzeugten elektrischen Ströme zu messen. Nach Begutachtung der Daten waren die Ärzte in der Lage, den Herzschlag mittels eines Chaos-Kontrollprogramms zu manipulieren“. Weitere Details stehen hier.

Wenn ich sage, dass Perioden-Verdoppelungs-Bifurkationen in dynamischen Systemen universell sind, übertreibe ich nicht – man versuche es selbst mit der einfachen Suche im Internet nach ,images bifurcation diagram‚. Klickt man sich durch die Ursprünge der resultierenden Bilder kann man eine Ahnung bekommen – man findet sie überall in nicht linearen, dynamischen Systemen – Biologie, Evolution, Chemie, Physik, Mathematik, Wärmefluss, strömende Flüssigkeiten, Manipulation des Herzschlags, das Studium und die Funktionen von Neuronen im Gehirn, verschiedene physikalische Oszillatoren, kartographische Erfassung und Kontrolle von Epidemien wie Masern, Sorgen von Ingenieuren hinsichtlich von Vibrationen in Strukturen und so weiter (also wirklich…).

Wie in Teil 2 dieser Reihe erklärt, wissen Ingenieure um das Chaos und führen umfangreiche Untersuchungen durch, damit ihre Systeme innerhalb der Parameter stabiler Regimes verbleiben. In einer Ingenieurs-Studie heißt es: „Chaos ist bei den meisten technischen Anwendungen unerwünscht. Viele Forscher haben sich dem Auffinden neuer Wege verschrieben, um Chaos effizienter zu unterdrücken und zu kontrollieren“.

Perioden-Verdoppelung führt zu Chaos

Weiter vorn in dieser Reihe habe ich Edward Lorenz mit den Worten zitiert „Ein Phänomen, dass man später ,Chaos‘ nennt – scheinbar zufälliges und unvorhersagbares Verhalten, das nichtsdestotrotz präzisen und oft sogar einfach zu formulierenden regeln folgt“.

[Einschub des Übersetzers: Ich selbst habe mich als Hobby ebenfalls mal mit der Chaos-Theorie beschäftigt. Man unterscheidet das ,deterministische Chaos‘, das dennoch strikt durchweg bekannten Gesetzen folgt, wie es der Autor hier beschreibt, und das ,absolute Chaos‘ wie z. B. der Flug eines Schmetterlings. Merkwürdig, dass der Autor diesen grundlegenden Unterschied hier nicht erwähnt.

Ende Einschub]

Er verwendet den Terminus Chaos, um Prozesse zu beschreiben, die „scheinbar zufällig fortschreiten, obwohl deren Verhalten strikt durch präzise Gesetze vorgegeben wird“. Er weitet die Definition aus auf „Phänomene, die leicht zufällig sind, unter der Voraussetzung, dass ihre viel größere offensichtliche Zufälligkeit nicht ein Nebenprodukt ihrer leichten wahren Zufälligkeit ist. Das heißt, Prozesse in der realen Welt, die so aussehen, als ob sie zufällig ablaufen – vielleicht ein fallendes Blatt oder eine flatternde Fahne – sollten ebenfalls als Chaos gelten, solange sie weiterhin zufällig aussehen, selbst falls irgendeine wahre Zufälligkeit irgendwie eliminiert werden kann“.

(Dieses definitorische Problem wird verschärft durch die Verwendung zahlreicher anderer Termini – Nichtlinearität, nichtlineare Dynamik, Komplexität und Fraktale – welche heute oftmals synonym verwendet werden mit Chaos im einen oder anderen Sinne. Und das als Clou auf der Tatsache, dass der Terminus ,Chaos-Theorie‘ eine Fehlbezeichnung ist – es handelt sich nicht um eine einzelne Theorie, sondern ein weites Feld für Studien, und betrifft Systeme, die durchweg deterministisch sind).

Unser Bifurkations-Diagramm zeigt, was passiert, wenn ein nicht lineares, dynamisches System über einen bestimmten Punkt hinausgeht – seien das nun Dynamik der Population, aerodynamische Flüsse oder der Bau von Brücken. Aufeinander folgende Perioden-Verdoppelungen führen zu Chaos – scheinbar zufälligem und unvorhersagbarem Verhalten – der nahezu durchweg grau gefärbte Teil der Logistischen Graphik. In einigen chaotischen Systemen kommt es zu period halving cascades gefolgt von Stabilität, diese wiederum gefolgt von aufeinander folgenden Perioden-Verdoppelungen. Die Wahrheit ist, dass dieses Verhalten IN KEINER WEISE zufällig ist, sondern strikt deterministisch. Aber an jedwedem und an allen gegebenen Punkten in dem chaotischen Bereich sind alle zukünftigen individuellen Werte unvorhersagbar. Sie können nicht bestimmt werden, ohne sie tatsächlich zu berechnen.

Versteckt im Chaos-Regime finden sich Bereiche mit periodischem Verhalten, in perfekter Ordnung. Man beachte auch, dass die Werte von x eingezwängt sind – bei einem r-Wert von 3,7 wird x nicht unter 0,2 und nicht über 0,9 liegen (auf einer einheitlichen Skala). Steigt r jedoch über vier, kann x jeden beliebigen Wert annehmen, in der gesamten Bandbreite, alles oder nichts, und alles dazwischen.

Was noch sonderbarer ist: wenn die Datenpunkte im chaotischen Bereich auf unterschiedliche Weise betrachtet werden, kann ein dynamisches System mit einem chaotischen Attraktor lokal instabil, global aber stabil sein: sind einige Sequenzen erst einmal in den Attraktor eingetreten, divergieren Nachbarpunkte voneinander, verlassen aber niemals den Attraktor. Solche unterschiedliche Betrachtungen können beispielsweise eine Zeitreihe von Differenzen der Werte zu jedem nachfolgenden Punkt sein, oder in mehreren Dimensionen. Dann zeigen sich sehr komplexe und mathematisch wunderschöne Beziehungen, Strange Attractors genannt.

Der Rössler-Attraktor ist ein Beispiel:

Der Rössler-Attraktor wurde von Otto Rössler im Jahre 1976 entworfen, „aber die ursprünglichen theoretischen Gleichungen stellten sich später als nützlich bei der Modellierung von Gleichgewicht bei chemischen Reaktionen heraus“.

Dave Fultz (1921-2002) arbeitete am berühmten Hydrodynamics Lab der University of Chicago. Dort „erdachte Dave klug und systematisch noch vor Aufkommen der numerischen Modellierung eine Anzahl von Labor-Anomalien, um Einsicht zu erlangen in viele komplexe atmosphärische Prozesse, am bedeutendsten der atmosphärischen allgemeinen Zirkulation. Seine ,dishpan‚-Experimente ergaben greifbare Beispiele von anderenfalls kaum verstandenen physikalischen Prozessen“. In seiner dishpan [Übersetzung nach LEO: Abwaschschüssel) fand er nicht nur die atmosphärischen Prozessen innewohnende Ordnung wie etwa dem Jetstream, sondern auch Dinge, die ihn verstörten. „Für eine organized person ist Chaos sowohl ein Objekt der Faszination, weil es so unterschiedlich daherkommt, als auch der Besorgnis“. Raymond Hide hat in Cambridge ähnliche Arbeiten durchgeführt, wobei diese Bilder des grundlegenden dishpan-Apparates sowie einige von deren Ergebnissen eingingen, einschließlich eines chaotischen Zustandes rechts.

Diese physikalischen Experimente wurden nahezu simultan in numerischen Modellen nachgebildet, einschließlich jenes berühmten Modells, das von Edward Lorenz entwickelt worden war.

Das Chaos-Problem in Klimamodellen

„Das Klimasystem ist ein gekoppeltes, nichtlineares chaotisches System“, und wenn jemand dieses System modelliert, besteht das Modell mathematisch aus verschiedenen Formeln für die nichtlineare Dynamik fließender Bewegungen, Wärmetransfer und so weiter.

Die Wärmetransfer-Gleichungen lauten:

Bemerkung zu Stefan-Boltzmann: „Thermische Strahlung bei Gleichgewicht wurde von Planck untersucht mittels gleichgewichts-thermodynamischer Konzepte. Die thermischen Eigenschaften des Gases aus Photonen sind bekannt. Eine davon, das Stefan-Boltzmann-Gesetz, gibt den Wert des Energieflusses mit den Termen der Temperatur des Emitters durch ein Kraftgesetz [power law]: σT4. Das klassische Schema ist nicht mehr anwendbar (beispielsweise wenn die Strahlung nicht im Gleichgewicht ist infolge der Gegenwart thermischer Quellen oder Temperaturgradienten). Dann wird es notwendig, eine Nicht-Gleichgewicht-Theorie heranzuziehen. Ein erster Versuch, Nicht-Gleichgewichts-Strahlung zu beschreiben könnte durchgeführt werden mittels Nicht-Gleichgewichts-Thermodynamik. Nichtsdestotrotz sind einige der Gesetze, die das Verhalten thermischer Strahlung bestimmen, nicht lineare Gesetze, deren Ableitung jenseits des Schirmes dieser Theorie liegen, die lediglich lineare Beziehungen bietet zwischen Flüssen und Kräften“. — Nonequilibrium Stefan-Boltzmann law,  Pérez-Madrid_ and Rubí (2010).

Und dann ist da noch die Boltzmann’sche Transport-Gleichung [Boltzman Transport Equation (BTE)], welche das statistische Verhalten eines thermodynamischen Systems beschreibt, das sich nicht im Gleichgewicht befindet. Ein klassisches Beispiel hierfür ist eine Flüssigkeit mit Temperaturgradienten wie etwa ein Ozean oder eine Atmosphäre. Darin fließt Wärme aus wärmeren zu kälteren Gebieten. „Die BTE ist eine nonlinear integro-differential equation, und die unbekannte Funktion in der Gleichung ist vermutlich eine Wahrscheinlichkeits-Dichte-Funktion im sechsdimensionalen Raum mit Geschwindigkeit und Lage eines Partikels. Das Problem der Existenz und Einheitlichkeit von Lösungen ist immer noch nicht vollständig gelöst, aber einige Ergebnisse aus jüngster Zeit sind vielversprechend. „Das Ausformulieren der Formel wird uns hier nicht erleuchten. Allerdings weise ich darauf hin, dass die Gleichung eine nichtlineare stochastische partielle Differentialgleichung ist, weil die unbekannte Funktion in der Gleichung eine kontinuierliche Zufallsvariable ist. (In einem stochastischen Prozess gibt es einige Unbestimmtheiten: selbst wenn die Ausgangsbedingung (oder der Startpunkt) bekannt ist, gibt es viele (oftmals unendlich viele) Richtungen, in die sich der Prozess entwickeln kann).

Und was auch auf das Klima anwendbar ist: Newtons Gesetz von Abkühlung

„Konvektive Abkühlung wird manchmal beschrieben als Newtons Gesetz von Abkühlung: Die Rate des Wärmeverlustes eines Körpers ist proportional zum Temperaturunterschied zwischen dem Körper und dessen Umgebung“.

Allerdings erfordert die Gültigkeit des Newton’schen Abkühlungsgesetzes definitionsgemäß, dass die Rate des Wärmeverlustes durch Konvektion eine lineare Funktion („proportional zu“) der Temperaturdifferenz ist, die den Wärmetransport antreibt, und bei konvektiver Abkühlung ist dies manchmal nicht der Fall. Allgemein ist Konvektion nicht linear abhängig von Temperaturgradienten und in manchen Fällen sogar stark nichtlinear. In diesen Fällen ist das Newton’sche Gesetz nicht anwendbar (zusätzlicher Link).

Die Navier–Stokes-Gleichungen beschreiben die Bewegung viskos flüssiger Substanzen. Sie werden zur Modellierung von Dingen wie Wetter und Ozeanströmungen herangezogen und sind nichtlineare partielle Differentialgleichungen im allgemeinen Fall und gelten daher auch für fast jede reale Situation. Die Nichtlinearität macht die meisten Probleme schwierig oder unmöglich zu lösen und ist der Hauptbeitragende zur Turbulenz, welche die Gleichungen modellieren.

Ich bin sicher, dass all jene, die diesen Blog oft besuchen, die Bedeutung dieser Formeln/Gesetze erkennen. Es kann verstörend sein zu bemerken, dass die Stefan-Boltzmann-Gleichung, das Newton’sche Abkühlungsgesetz und Navier-Stokes-Gleichungen der Dynamik von Flüssigkeiten tatsächlich nicht linear sind, sondern dort, wo die Ozeane auf die Atmosphäre treffen, allesamt in ihrer Natur und ihrem Verhalten nichtlinear sind (hier). Diese sind Teil der vielen anderen nichtlinearen dynamischen Systeme, die bei der Klimamodellierung involviert sind.

Die in der täglichen Wissenschaft verwendeten linearen Versionen, einschließlich der Klimawissenschaft, sind oftmals nichts weiter als vereinfachte Versionen der wirklichen Phänomene, die sie beschreiben sollen – vereinfacht, um die Nichtlinearitäten einzuschränken oder zu entfernen. In der realen Welt, der sich nicht im Gleichgewicht befindlichen Welt, verhalten sich Klimaphänomene nichtlinear im Sinne nichtlinearer dynamischer Systeme. Warum aber verwenden wir diese vereinfachten Formeln, falls sie nicht akkurat die reale Welt reflektieren? Weil die Formeln, die die reale Welt akkurat beschreiben, nichtlinear sind und viel zu schwierig – oder unmöglich – zu lösen sind – und selbst wenn sie lösbar wären, würden sie Ergebnisse zeitigen, die unter normalen Bedingungen mit einem Wort unvorhersagbar und hoch sensitiv gegenüber den Ausgangsbedingungen (hier) sind. Nicht alle Formeln können adäquat vereinfacht werden, um die Nichtlinearität zu entfernen.

Diese Beispiele sollen illustrieren, immer neu wiederholen und daran erinnern, dass viele der physikalischen Prinzipien und der mathematischen Formeln, die diese Prinzipien beschreiben, in ihrer ursprünglichen und geeigneten Form nichtlinear sind, da sie nichtlineare dynamische Systeme repräsentieren. Und diese Formeln finden Eingang in die allgemeinen Zirkulationsmodelle, die Wetter, Klima und Klimawandel vorhersagen sollen.

Das Ergebnis dieser Lage sind Modellsimulationen, die genau wie dieses Multi-Model-Ensemble der Wintertemperaturen in der Arktis aussehen, überlagert mit einer CRUT2.0-Version der gemessenen Temperaturen:

Der Begleittext zeigt, dass „alle drei Läufe von einem der Modelle (violette dünne Linien mit offenen Dreiecken) mit relativ warmen Zuständen begonnen haben, im Gegensatz zu Simulationen anderer Modelle und Beobachtungen. Die Simulation von Meereis durch dieses Modell zeigt offensichtlich eine ungeeignete Initialisierung für die Simulation des Klimas im 20. Jahrhundert (Zhang and Walsh 2006). Eine andere Erklärung ist, dass sich das Modell immer noch in einem Nicht-Gleichgewichts-Zustand befindet (Y. Yu 2005, IPCC Workshop, persönliche Unterhaltung). Aus diesem Grunde werden die Ergebnisse vom FGOALS-g1.0 aus der Statistik und den Diskussionen in den folgenden Abschnitten ausgeschlossen“. Mit anderen Worten, obwohl das allgemeine Bild eines von vielen jeweiligen Läufen von 20 Modellen ist, wobei jeder Lauf klassisch nichtlineare, chaotische Ergebnisse liefert, waren die FGOALS-Läufe so weit entfernt davon, synchron mit den Anderen zu sein, (aus noch nicht völlig verstandenen Gründen), dass sie einfach weggeworfen werden mussten – nicht weil es sich um ein schlechtes Modell handelt – sondern aufgrund der grundsätzlich nichtlinearen Natur der Physik des modellierten Klimas – die Physik ist extrem sensitiv gegenüber Ausgansgbedingungen, und wenn wir lediglich „die Mathematik ausführen“, ist das Ergebnis – das Chaos in ihrem Wesen – kaum eingeschränkt.

Alles in allem erkennt man, dass es eine Art eines grünlich-bläulich konzentrierten Bandes zu geben scheint, das von 1880 bis 2000 läuft mit einem Startwert bei -0,3 und endend bei +0,3, welches etwa 0,4 Grad breit aussieht. Ich habe den Verdacht, dass dies auf der Grundlage – oder ein Artefakt einer – gewissen Übereinstimmung von Parametern zwischen den Modellen beruht. Dies sollte nicht verwechselt werden mit einer übereinstimmenden Vorhersage/Projektion. Es ist in der Klimawissenschaft Standardpraxis, alle jene (Arten von) zitternden Linien (Modellergebnisse) zu „mitteln“ und das eine „Projektion“ zu nennen. Warum das absurd ist, wird deutlich, wenn man diesen Beitrag liest: Real Science Debates Are Not Rare, ein Gastbeitrag hier bei WUWT von Dr. Robert G. Brown im Oktober 2014.

Diese Diskussion über Modelle beabsichtigt in keiner Weise, ein Angriff auf Modelle allgemein zu sein, sondern sie soll lediglich darauf hinweisen, dass die Ergebnisse derartiger Modelle der Output gekoppelter nichtlinearer chaotischer Systeme sind und folglich drastisch unterschiedliche Ergebnisse für das gleiche Problem liefern, mit den gleichen physikalischen Formeln, unter Verwendung sich geringfügig unterscheidender Modelle für das gleiche Klimasystem mit den im Wesentlichen gleichen Ausgangsbedingungen.

Die Ergebnisse des obigen Modelllauf-Ensembles „prophezeien nicht“ die bekannte Vergangenheit mit irgendeinem Grad von Genauigkeit und zeigen sogar die offensichtlichen Höhen und Tiefen nicht. Der Hauptgrund hierfür ist nicht, dass die Modelle unrichtig und unvollständig sind – sondern dass sie korrekt genug sind, um zumindest Einiges der Nichtlinearität des realen Klimas zu enthalten. Folglich erzeugen sie Ergebnisse, die 1) sich wild über die gesamte Bandbreite erstrecken, abhängig von Ausgangsbedingungen, und 2) sich jedes Mal unterscheiden, wenn man sie laufen lässt mit irgendeiner anderen als genau der gleichen Ausgangsbedingung ohne jede Variation – beide diese Fakten sind Seiten der gleichen Medaille – Chaos.

Wenn man also durch die Linse der Chaos-Theorie schaut – der Linse des Studiums nichtlinearer dynamischer Systeme – ist es nahezu unsinnig zu sagen, dass die „(Klima-“)Modelle in Übereinstimmung sind.

Aber Moment, einige könnten sagen, dass ein bläulich-grünes Band und die Steigung auf der rechten Seite … uns sicher etwas sagen kann, dass die Modelle darin übereinstimmen, dass die Temperatur allgemein steigen wird und schneller steigen wird, je näher man der Gegenwart kommt. Die Antwort hierauf aus der Chaos-Theorie ist es, darauf hinzuweisen, dass den grundlegenden Gleichungen Parameter hinzugefügt worden waren, um dieses Ergebnis sicherzustellen – dass das Modell „frisiert“ worden war zu „funktionieren“ – Frisiert, um zumindest allgemein dieses Ergebnis zu erzeugen. Würde das Modell nämlich die Vergangenheit nicht einmal annähernd reproduzieren, die bekannten Beobachtungsdaten, würde das Modell als falsch angesehen – um aber das Modell als korrekt zu beurteilen oder es überhaupt als gerechtfertigt anzusehen, muss es dieses allgemeine Bild erzeugen, um mit einem Jahrhundert bekannter Beobachtungsdaten „übereinzustimmen“.

Es ist dieses Frisieren, um es „passend“ zur jüngsten Vergangenheit zu machen, das die Modelle darin einschränkt, mit steigendem CO2 eine Zunahme zu erzeugen – es ist einfach Teil der Formel, die verwendet wurde, um das Modell in allen Fällen zu erzeugen. In unserem Beispielbild unten wären die Modelle, wenn sie nicht Projektionen geliefert hätten, die ähnlich aussahen wie im Zeitraum 1980 bis 1999, so lange re-frisiert worden, bis sie genau dieses Ergebnis hervorbringen würden. Ohne dieses Frisieren sagt uns die Chaos-Theorie, dass die Modelle Ergebnisse liefern würden, die mehr der rechten Seite dieses Bildes ähneln, wo die Temperatur immer noch chaotisch ist, aber wie auch immer man es dreht und wendet, die Temperatur nicht frisiert/parametrisiert worden ist, um automatisch mit dem CO2 zu steigen. (Die blaue Linie repräsentiert die Mittellinie der Projektionen zum Jahr 2000 (dem Beginn der „Zukunft“ für diese Läufe).

Ich habe in Part 2 dieser Reihe gezeigt, wie einfach diese Art von Frisieren erreicht werden kann, was zu diesen beiden Bildern führt:

In der kleinen oberen Graphik, die ich innerhalb von 10 Minuten erstellt hatte, verwendete ich die einfachste aller nichtlinearen Formeln (die logistic equation), wobei ich den Antrieb (das „r“ in der Formel) leicht verändert habe, so dass es minütlich zu- und abnimmt – um lediglich ein Tausendstel Grad pro Jahr, auf oder ab während verschiedener Zeiträume (wobei ich mein Modell grob an die globale mittlere Festlandstemperatur von 1856 bis 2014 angepasst habe). Zu diesem Ergebnis habe ich dann eine Hinzufügung addiert, die zufällig variiert zwischen 2 und 6 Prozent. Überlagert man meine frisierte chaotische Graphik den realen Beobachtungen, zeigt sich das fit. Ich beweise hier nichts bzgl. Klima, sondern nur, wie einfach, wie trivial es ist, selbst eine bekannte nichtlineare Formel so zu parametrisieren, dass ein bekannter Datensatz simuliert wird.

Wie wir sehen, ist es möglich, dass die Parameter, das Frisieren von GCMs den Haupt-Kontrollfaktor des Aussehens und der Richtung der Modellergebnisse repräsentieren kann.

Ich bin mir ziemlich sicher, dass das Frisieren/die Parametrisierung eines GCMs viel komplexer und schwieriger ist und außerdem – wie wir am Beispiel der Wintertemperaturen in der Arktis sehen – nicht immer erfolgreich ist.

Einige (auf der Seite der Klima-Abweichler) charakterisieren dieses Frisieren, diese Parametrisierung der Klimamodelle als eine Art des Schummelns. Aber das ist es nicht. Es ist einfach ein notwendiger Schritt, falls die Modelle für überhaupt etwas brauchbar sein sollen. Es ist dieser Notwendigkeit geschuldet, dass die wirklichen Auswirkungen einer solchen Parametrisierung vollständig bekannt gemacht werden müssen, wenn man die Ergebnisse der Modellläufe und Ensembles interpretieren will – etwas, von dem viele glauben, dass es in den derzeitigen klimawissenschaftlichen Diskussionen fehlt. Jene Bekanntmachung muss begleitet sein von der Bekanntmachung der wirklichen Bedeutung der zugrunde liegenden Nichtlinearitäten und folglich der gesamt-Limitierungen der Modelle selbst.

Einige Klimawissenschaftler, Mathematiker und Statistiker sind der Meinung, dass es einfach nicht möglich ist, Modelle auf der Grundlage multipler gekoppelter (voneinander abhängiger) nichtlinearer dynamischer Systeme zu verwenden, wobei jedes sehr stark von seinen eigenen Ausgangsbedingungen abhängt. Man verändere sie ein wenig und gieße bedeutsame Projektionen oder Prophezeiungen zukünftiger Klimazustände aus – oder sogar Vergangenheit oder Gegenwart. Sie fühlen, dass es sogar noch unwahrscheinlicher ist, dass die Vermengung oder Mittelung multipler Modellprojektionen Ergebnisse erzeugen kann die zu jeder Art objektiver Realität passen – vor allem der Zukunft.

Der Autor: Bevor dieser Beitrag kommentiert wird:

Erstens, ich lehne es nach wie vor ab, mich in irgendeiner Art und Weise darüber zu streiten, ob das Klima der Erde ein „gekoppeltes, nichtlineares chaotisches System“ ist oder nicht. Vielmehr biete ich die folgende Liste mit Links an, die nicht mit mir übereinstimmen und für jeden, der mehr wissen möchte über die Chaos-Theorie und deren Implikationen:

The Essence of Chaos — Edward Lorenz
Does God Play Dice ? — Ian Stewart
CHAOS: Making a New Science — James Gleick
Chaos and Fractals: New Frontiers of Science — Peitgen, Jurgens and Saupe

Additional reading suggestions at Good Reads (skip the Connie Willis novella)

Zweitens, bevor man sich darüber auslässt, wie das Klima „nicht chaotisch ist“ oder der und der Datensatz „nicht chaotisch ist“, gehe man noch einmal zurück zu den Definitionen zu Beginn dieses Beitrags.

…

Link: https://wattsupwiththat.com/2016/09/04/chaos-climate-part-3-chaos-models/

Übersetzt von Chris Frey EIKE



Jagen wir IMAGINÄREN Zahlen nach?

geschrieben von Kip Hansen | 12. Oktober 2016

[Vorab-Hinweis des Übersetzers: In diesem Beitrag gibt es viele verschiedene Hervorhebungen. Alle diese Hervorhebungen sind aus dem Original!]
Anfang Oktober hat der unermüdliche Willis Eschenbach von WUWT einen Gastbeitrag veröffentlicht, in dem er sich einen Radiobericht vorknöpft von Ira Flatow, der sich unter dem Motto zusammenfassen lässt „Einige jüngste Überschwemmungen in Miami, Florida, sind der Beweis, dass der Klimawandel real ist und Florida bereits beeinflusst“. Als Erwiderung auf einen Kommentar von mir zu diesem Beitrag stellte Eschenbach diese sehr interessante Frage:
„…wie Sie sagen, wir können den Meeresspiegel mit einem „hohen Grad an Genauigkeit“ vermessen … messen wir also etwas Imaginäres? Und falls wir jene hoch akkuraten Messungen mitteln, warum bekommen wir nicht einen globalen mittleren Meeresspiegel? Was übersehe ich hier?“
In der Wissenschaft gilt, dass das Stellen der richtigen Frage oftmals, vielleicht immer, wichtiger ist als die richtige Antwort. Schauen wir mal auf Eschenbachs Fragen um herauszufinden, was in der Welt und in der Welt der Wissenschaft los ist.
Um welche Fragen geht es hier?
1. Können wir den Meeresspiegel mit einem „hohen Grad an Genauigkeit“ messen?
2. Messen wir etwas Imaginäres (wenn wir das tun)?
3. Falls wir jene hoch akkuraten Messungen mitteln, warum bekommen wir nicht einen globalen mittleren Meeresspiegel?
4. Was übersehe ich hier?
Hier kommt mir der Gedanke, eine allgemeinere Frage zu stellen – was messen wir in der Klimawissenschaft, und: messen wir etwas Imaginäres, wenn wir das tun? – Aber wir können „Meeresspiegel“ als Beispiel für das Gedankenexperiment heranziehen.
Zuerst zur ersten Frage: Ist es wirklich möglich, so etwas wie den Meeresspiegel (oder die Lufttemperatur in 2 m Höhe oder die Wassertemperatur) mit „einem hohen Grad an Genauigkeit“ zu messen?
Als ich in meinem Originalkommentar feststellte, dass wir seit Jahren den Meeresspiegel mit einem hohen Grad an Genauigkeit gemessen haben, wollte ich damit sagen, dass wir wussten, welcher Meeresspiegel an verschiedenen Plätzen in Zukunft zu erwarten wäre. Hintergrund war der Gedanke, was ein allgemeinerer „globaler Meeresspiegel“ wohl sein könnte und welche Änderungen über längere Zeiträume hinweg wie dem vorigen Jahrhundert oder so aufgetreten sein könnten. Aber für unser Gedankenexperiment in diesem Beitrag wollen wir „hoher Grad an Genauigkeit“ definieren als die üblicherweise erwähnte „jährliche Anomalie“ in der wissenschaftlichen Literatur. Für „globalen mittleren Meeresspiegel“ sind diese einstellige Millimeterzahlen, gewöhnlich 1,7 oder 1,8 mm bis zu 3,4 mm pro Jahr, irgendwo in diesem Bereich. (…)
Bevor wir sehr viel weiter gehen, wollen wir fragen „warum wollen wir (sie) den globalen Meeresspiegel messen“? Der Hauptgrund scheint es in unserer politisierten Welt der Globale-Erwärmung-Politik zu sein, dass Viele ihn messen wollen um zu zeigen, dass er steigt (was er schon seit einiger Zeit tut, zumindest während der letzten 20.000 Jahre) und dass dieser fortgesetzte Anstieg 1) gefährlich und 2) dem jüngsten Temperaturanstieg während des vorigen Jahrhunderts geschuldet ist und 3) folglich nur die globale Erwärmung dafür in Frage kommt. Das Motto lautet, den Anstieg des Meeresspiegels auszuschlachten als einen Beweis für die zunehmende thermische Ausdehnung des Wassers sowie der zunehmenden Hinzufügung von Wasser durch schmelzende Landeismassen. Beides soll vermeintlich die Folge der globalen Erwärmung sein, verursacht durch steigende atmosphärische Konzentrationen von Treibhausgasen, hauptsächlich CO2, seit den achtziger Jahren des 19.Jahrhunderts. Wir werden später in diesem Beitrag sehen, dass dies Bestandteil einer größeren modernen wissenschaftlichen Bewegung ist, um „Einzelzahlen“ zu erzeugen, die dynamische Systeme repräsentieren sollen (wobei man von einigen davon weiß, dass sie nichtlineare dynamische Systeme sind).
Können wir den Meeresspiegel bis zu jener Genauigkeit von ± 3 bis 4 mm messen? Nun, für den Meeresspiegel lautet die Antwort selbst an einer einzigen präzisen Stelle Nein, können wir nicht!“ Nein, ich versuche hier nicht, provokativ zu sein – es ist schlicht und ergreifend eine Tatsache. Falls das Meer so freundlich wäre und stillstehen würde, selbst nur für wenige Augenblicke, könnten wir mit einer sehr genauen Messung an einer einzelnen Stelle oder vielleicht auch vielen Stellen aufwarten. Aber ach, das Meer ist niemals ruhig, es bewegt sich immer auf- oder abwärts: Gezeiten Strömungen, Wellen, Schiffe, steigender bzw. fallender Luftdruck und – an den meisten Stellen – alles zusammen. Folglich können wir es aus physikalischen Gründen nicht; das Meer ist einfach nicht lange genug ruhig, um diese Messung bis zu diesem Genauigkeitsgrad durchführen zu können. Das wird sogar noch schlimmer, wenn wir dieser Information sowohl das Land selbst als auch den Meeresgrund hinzufügen, die sich fast überall in vertikaler Bewegung befinden und emsig dabei sind, die Volumina der Ozeanbecken zu verändern.
Viele werden protestieren: „Schauen Sie mal hier, Mr. Hansen, das können Sie nicht sagen. Es gibt eine Unmenge sehr wissenschaftlicher Tabellen, Graphiken und Zeitschriftenartikel, die uns sehr sorgfältig darüber belehren, dass wir jene Messung nicht nur durchführen können, sondern das wir das auch getan haben über lange Zeiten der menschlichen Historie und seit 1992 mit Satelliten!“
Mein Punkt hier lautet, dass das, was wir tun und wo wir es tun, keine Messung ist, sondern Ableitung. Viele Messungen werden durchgeführt, an vielen und unterschiedlichen Stellen zu verschiedenen und unterschiedlichen Zeiten. In einigen Fällen gibt es fast kontinuierliche Zeitreihen von Messungen für bestimmte Stellen. Von diesen zahlreichen individuellen Messungen misst beispielsweise die Tidenstation am Battery Park in New York City, dann wird eine interessante Formel zur Anwendung gebracht, um eine Zahl abzuleiten, die die mittlere Differenz zwischen der Meeresoberfläche und einem geodätischen Punkt über einen bestimmten Zeitraum repräsentiert. Der Punkt wurde schon vor Jahren im Felsgrund von Manhattan Island errichtet. Wir werden die fast infinitesimalen Details weglassen, ob die abgeleitete Zahl einen einfachen Mittelwert zwischen Höhen und Tiefen repräsentiert oder ob es ein Mittelwert mit der Zeit ist.
Ich möchte hier darauf hinweisen, dass das NOAA CO-OPS-System von Tidenstationen ein wichtiges und pragmatisches Ziel hat. Schiffe und Boote müssen die Wassertiefe an einer bestimmten Stelle kennen – auf einem Dock im Hudson River oder auf einer Sandbank in der Bucht – und zu einer bestimmten Zeit. Folglich sind die Gezeitentabellen für zur See fahrende kommerzielle Schiffe und auch Freizeitboote sehr wichtig. Wichtige Fragen werden durch sie beantwortet, etwa: „Kann ich dorthin fahren ohne diese bösen Felsen auf dem Grund zu berühren? Kann ich dort bleiben, ohne dass mich die Gezeiten auf den Felsen am Grund absetzen?“ Dieses System war niemals dafür gedacht, den „Anstieg des Meeresspiegels“ zu messen. Nichtsdestotrotz wird es jedoch herangezogen, um Änderungen des relativen Meeresspiegeltrends zu berechnen. Zwei Artikel bei Wikipedia hierzu gibt es hier und hier. Im zweiten Artikel findet sich die folgende Abbildung:

Man beachte bitte die Differenz zwischen dem Trend berechnet aus Tidenmessungen (orange Linie mit grauer Fehlerbandbreite) und den blauen Satellitenmessungen. Daten von Tidenmessungen (welche den Relativen Meeresspiegel an jeder Messstelle zeigen) zeigen einen sich beschleunigenden Anstieg, während Satellitendaten, welche den absoluten Meeresspiegel messen, bei dem seit einem Jahrhundert zu beobachtenden Trend bleiben.
Aber was ist mit diesen wunderbaren Satelliten? Die offizielle NOAA-Behauptung lautet: „Eine Reihe von Satelliten-Missionen, die mit TOPEX/Poseidon im Jahre 1992 begannen und mit Jason-1 (2001 bis 2003) und Jason-2 (2008 bis heute) schätzen den globalen mittleren Meeresspiegel alle 10 Tage mit einer Unsicherheits-Bandbreite von 3 bis 4 mm“. Ergebnisse in graphischer Form kann man der Website der NOAA Laboratory for Satellite Altimetry einsehen. Es ist interessant, den Unterschied sichtbar gemacht zu sehen, der sich aus dem Gebrauch alternativer Kolorierungs-Schemata ergibt sowie die klumpige Beschaffenheit [lumpiness ?] der Ozeane.

Ich weiß, dass viele Leser hier mit dem Meer vertraut sind – Willis Eschenbach und ich selbst haben einen großen Teil unseres Lebens auf dem Meer verbracht und einen sogar noch größeren Teil am Rande der Meere. Drei oder vier Millimeter, das ist etwa die Dicke von zwei amerikanischen Pennies übereinander gelegt. Es ist selten und schön sowie äußerst inspirierend, den Ozean glatt wie eine Butterstulle bis zum Horizont zu sehen, oder auch nur über eine Bucht oder einen Hafen hinweg. In meinen 20 Jahren, auf dem Meer habe ich nur sehr selten eine so ruhige See gesehen – die kleinste Brise bringt Rippelwellen weit über 3 bis 4 mm hinaus. Diese Wellen können sich rasch auf Zentimeter und Meter hochschaukeln. Falls ein Wasserreservoir zum Ozean hin offen ist, wandern schwingende Ozeanwellen von einem Horizont zum Anderen, und nicht immer unbedingt in der Richtung, in der der Wind weht. Dies alles addiert sich zu einer großen vertikalen Bewegung der Meeresoberfläche – manchmal anregend, manchmal einfach zum Fürchten.
Falls also die NASA behaupten möchte, dass deren Satelliten in ihren perfekten Orbits irgendwie die sich ständig ändernde, unebene Oberfläche der Ozeane der Welt zu einer Auflösung von ± 3 bis 4 mm transformieren kann, dann bitte sehr. Wer bin ich, der ich zu sagen wage, dass sie das nicht kann, selbst falls ich mir nicht vorstellen kann, wie sie das selbst theoretisch tun könnten. Wie auch immer, für unsere Zwecke hier möchte ich folgende Unterscheidung treffen: sie messen den globalen Meeresspiegel alle 10 Tage nicht – sie behaupten das noch nicht einmal. Ihre Behauptung lautet, dass sie ihn schätzen. In jeder wirklich pragmatischen Hinsicht leiten sie irgendwie eine einzelne Zahl aus einer sagenhaft großen Datenmenge ab – Daten, die selbst keine direkten Messungen sind, sondern Rückschlüsse aus anderen Datenarten.
Aber zurück zu Ernsterem. Obwohl es möglich wäre, den Meeresspiegel an individuellen Stellen zu messen, ist dies schwierig; und selbst wenn man das tut, ist es keine wirkliche Messung, sondern eine Ableitung aus akkumulierten Daten und Abhängig von mathematischen und statistischen Verfahren und Definitionen. Falls man jemals eine spezielle Sektion des Meeres „auf Meeresspiegel-Höhe“ findet, wäre dies total augenblicklich und zufällig.
Der Meeresspiegel, selbst der „Meeresspiegel am Battery-Park in New York“ wird nicht angemessen repräsentiert durch eine einzelne Zahl über und unter irgendeiner geodätischen Eckmarke. Was wir Meeresspiegel nennen, ist eine abgeleitete, berechnete Zahl – Ein Mittel von Mittelwerten eines Bündels von Messungen und Zeitreihen. In dieser Hinsicht ist die Zahl als berechneter Mittel-Punkt einer Bandbreite mit der Zeit, im praktischen Sinne eine imaginäre Zahl, die im Alltagsleben des Hafens von New York keine Existenz aufweist.
Es gibt jedoch einen „pragmatischen Meeresspiegel am Battery-Park in New York“ – welcher selbst eine vorhersagbare Bandbreite über und unter irgendeiner Wassertiefe an einem bestimmten Punkt ist (den man als den Mittleren Meeresspiegel vor Ort [Local Mean Sea Level] bezeichnet), den man modifiziert durch erwartete, vorhergesagte Gezeiten extrapolieren kann auf andere Punkte in dem Hafen. Das ist für Seefahrer nützlich, trotz seines Weniger-Als-Real-Aspektes. Er kann verwendet werden in Rohform (Bruchteile von Metern), um die Wassertiefe zu bestimmen über Grund an einer Stelle und zu einer Zeit, die für Kapitän und Mannschaft eines Schiffes von Interesse ist. Hier folgt die Vorhersage von Wasser-Niveaus relativ zum MLLW vom 9. bis zum 11. Oktober:

Unter dem Strich steht, dass der Meeresspiegel, überall und zu irgendeiner Zeit, keine direkte Messung ist. Niemals. Es ist eine berechnete, abgeleitete Zahl, die einen präzise definierten, aber tatsächlich ziemlich komplizierten Gedanken zur Grundlage hat.
Um einen globalen Meeresspiegel zu definieren, muss man sich in Imagination üben entlang folgender Umrisse: Man stelle sich vor, dass der Planet aufgehört hat zu rotieren; dass der Mond niemals existiert hat; dass der Planet eine perfekte Sphäre ist; dass kein Wind weht; dass die Atmosphäre gleichmäßig verteilt und der Luftdruck überall gleich ist; dass die Wassertemperatur der Meere genau gleich ist, überall und in allen Tiefen; dass es keine Strömungen gibt und keine Eiskappen; dass die Flüsse aufgehört haben, ins Meer zu fließen und dass die Gravitation wie durch Zauberhand an allen Punkten der Erde genau gleich ist (dem ist mitnichten so). Unterall diesen Bedingungen könnten wir sagen, dass der globale Meeresspiegel präzise „da“ ist, innerhalb von 3 oder 4 mm. Liebe Freunde, DAS ist es, was den globalen mittleren Meeresspiegel in dieser speziellen Hinsicht zu einer imaginären Zahl macht.
Also haben wir jetzt Frage 2 beantwortet: Messen wir etwas Imaginäres (wenn wir das tun)? Ja, wir „messen“ in gewisser Weise etwas Imaginäres, wenn wir sagen, dass wir den Meeresspiegel messen. Die sich daraus ergebende berechnete, abgeleitete Zahl ist ein Produkt unserer Vorstellungen, eine imaginäre Zahl.
Frage 3 beantwortet sich fast von selbst. „Falls wir jene hoch genauen Messungen mitteln, warum bekommen wir dann keinen globalen mittleren Meeresspiegel?“ Man kann eine sinnverwirrende Vielfalt statistischer und mathematischer Schritte vornehmen und zu irgendeiner Zahl kommen – je mehr Schritte man vornimmt, umso präziser wird die Zahl aussehen. Man kann jedweden Datensatz mitteln. In diesem Falle – wird man eine Zahl erhalten, die der „mittlere globale Meeresspiegel“ ist? Schauen wir aber erst mal auf Frage 4, bevor wir hierauf noch einmal zurückkommen.
Frage 4 lautete: „Was übersehen wir (ich) hier?“
Das ist eine Frage der Logik und folgt irgendwie einem früheren Beitrag von mir hinsichtlich der „Unsicherheits-Bandbreiten“ (Uncertainty Ranges). Wenn man eine Reihe von Zahlen mittelt, von denen jede einzelne in Wirklichkeit eine Bandbreite repräsentiert, muss das Ergebnis ebenfalls eine Bandbreite sein. In unserem Falle hier muss das Ergebnis einer Mittelung einer von Computern ausgespuckten Masse von imaginären Zahlen eine andere imaginäre Zahl sein, in der gleichen Weise wie die Zahlen im Original-Datensatz. Man kann Messfehler im Original nicht hinweg mitteln, ebensowenig wie die Tatsache, dass die Ausgangsdaten selbst in Wirklichkeit Bandbreiten und nicht einzelne Zahlen sind. Und man kann auch nicht die Tatsache hinweg mitteln, dass die Originalzahlen im hier diskutierten Sinne imaginär sind.
Bevor wir hier zu weit abschweifen, möchte ich noch einmal klarstellen, wo ich die Unterscheidung sehe zwischen einer realen Zahl und dem, was ich hier eine imaginäre Zahl nenne. Diese Diskussion läuft ab vor dem Hintergrund der Messungen von Charakteristika der physikalischen Welt. Wenn das Ergebnis einer Messung eine reale Zahl sein soll, muss das Gemessene selbst messbar sein, und das diese Messung repräsentierende numerische Ergebnis muss etwas repräsentieren, das in irgendeiner Weise bedeutsam und nützlich existieren muss. Allerdings ist das Ergebnis einer Messung von etwas, dass selbst nicht physikalisch messbar ist, sondern nur auf der Grundlage einer mathematischen Definition abgeleitet werden kann, ein Gegenstand unserer Vorstellungen (etwas, dass in der realen Welt nicht wirklich zu finden ist). Dann sollte dieses Ergebnis in dieser speziellen Hinsicht ebenfalls als imaginär angesehen werden, trotz der vermeintlichen Präzision.
Es gibt unzählige Mittelwerte von Dingen, die abgeleitet und berechnet werden können. Unabhängig davon sind viele jener Mittelwerte selbst imaginär, und deren Bedeutung und Nützlichkeit muss immer sorgfältig bedacht werden. Derartige imaginäre Zahlen können einige interessierende Bedeutung haben, andere eine gewisse pragmatische Nützlichkeit, aber man muss sehr vorsichtig sein bei der Anwendung dieser Zahlen, weil sie – alles in allem – imaginär sind und in der realen Welt nicht existieren.
Folglich kann die mittlere Körpergröße amerikanischer Bürger nützlich sein bei der Bestimmung der Bettengröße, die man den Amerikanern verkauft, oder zumindest kann man eine Bandbreite betrachten. … Hingegen wäre es närrisch, mit so einer Zahl Bedrohungen der öffentlichen Gesundheit zu belegen, wenn sich eine solche Zahl auch nur geringfügig ändert über einen eng gefassten Zeitraum.
Noch schlimmer ist – und ich hoffe, dass zumindest dieser Gedanke Zustimmung finden wird – einfache Mittelwerte von Mittelwerten von Mittelwerten (die alle mit gemittelten, imaginären, abgeleiteten Zahlen anstatt mit tatsächlichen Messungen beginnen), sind grässliche Absurditäten (z. B. Simpson’s Paradox, etc.)
Hier folgt ein lächerliches Beispiel: Falls wir die mittlere Höhe des Landes im Bundesstaat South Carolina über NN berechnen und dabei erst die Höhe jedes Landkreises, dann die Höhe von Regionen mit mehreren Landkreisen und schließlich regionale Höhen mitteln, würde das Ergebnis eine Zahl sein von (einfach Pi mal Daumen) 125 Fuß [ca. 38 m] über dem Meeresspiegel. Wenn man dann einen Trend ermittelt vom höchsten Punkt in den Blue Ridge Mountains zum Meer, könnte man sagen, dass der Staat ein Gefälle von XX Fuß pro Meile aufweist. Es ergibt in dieser Hinsicht keinen Unterschied, falls wir die Mittelwerte wichten, die fehlenden Punkte irgendwie ersetzen oder das Ganze homogenisieren oder glätten. Diese Prozedur berechnet und/oder leitet eine imaginäre Zahl ab im genauen Sinne unserer Arbeitsdefinition hier. Folglich könnte man mit unserer magischen neuen imaginären Zahl behaupten: während einige Gebiete von South Carolina durch extreme Fluten zusammen mit 600 l/m² Regen überschwemmt werden könnten, würden die Menschen dort im Mittel keiner Katastrophe ausgesetzt sein, selbst wenn die wenigen Gebiete mit der erwarteten Überflutung rasch im Atlantik versinken würden. Die Anwendung einer solchen mathematisch absolut korrekten, jedoch imaginären Zahl in der realen Welt kann zu abwegigen Schlussfolgerungen führen. Es war genau diese von der Macht imaginärer Zahlen getriebene Logik, dass einen Journalisten der New York Times irrig behaupten ließ, dass der durch die globale Erwärmung steigende Meeresspiegel (ein wirklicher Anstieg, aber mit einer imaginären Zahl) erhebliche Schäden in New York City durch den Hurrikan Sandy verursacht habe. Den gleichen Fehler machte Ira Flatow hinsichtlich einer Überschwemmung in Miami, wo die Überschwemmung, auf die sie sich bezog, an einer Stelle erfolgte, die unter der langfristigen mittleren Hochwasser-Marke lag. Das war auch schon so, als die Straße gebaut worden ist.
Und jetzt zurück zu Frage 3: „Falls wir jene hoch akkuraten Messungen mitteln, warum bekommen wir keinen mittleren globalen Meeresspiegel?“ Falls wir den sehr großen Datensatz imaginärer Zahlen zu einem speziellen Zeitpunkt mitteln, werden wir eine neue, womöglich noch imaginärere Einzelzahl erhalten, die man, wenn jeder dem zustimmen kann, den „mittleren globalen Meeresspiegel“ nennen könnte. Wäre diese Zahl pragmatisch, praktisch, bedeutsam und nützlich? Vielleicht, aber dann nur in sehr begrenztem Maße … und wir müssten sehr sorgfältig überlegen, welche Bedeutung wir dieser Zahl beimessen.
Warum? Dazu schaue man auf meinen Beitrag vom vorigen Jahr (hier) über Hurrikan Sandy und den Schäden in NYC. Der proklamierte Anstieg des Meeresspiegels in dem 50-jährigen Zeitraum von 1960 bis 2010 „getrieben durch die globale Erwärmung“ sollte etwa 4 Inches [ca. 10 cm] betragen haben (etwa die Hälfte der 8 Inches im vergangenen Jahrhundert). Die Wirklichkeit ist: nur wenn wir die niedrigste Schätzung des Absinkens für den Battery Park koppeln mit der höchsten Schätzung der lokalen relativen Änderung des Meeresspiegels, sehen wir irgendeinen positiven Beitrag der absoluten globalen Änderung des Meeresspiegels am Battery Park: die 0,59 Inches [ca. 15 mm] in der oberen rechten Ecke:

Was ist hier los? Der akzeptierte geschätzte Anstieg des Meeresspiegel über ein Jahrhundert zeigt sich am Battery Park nicht, nicht einmal über die letzte Periode von 50 Jahren. Dies sollte uns nicht überraschen – Versuche, eine einzelne Zahl, den „globalen Meeresspiegel-Anstieg“ anzuwenden, ist völlig abwegig – und gleicht der Anwendung einer imaginären Zahl auf eine reale Situation.
Die heutige Diskussion ist eine Möglichkeit, auf den gegenwärtigen Trend in der Wissenschaft zu schauen, in der Versuche gemacht werden, sehr komplizierte dynamische Systeme auf eine Einzelzahl zu reduzieren, die man dann graphisch über die Zeit darstellen kann, für gewöhnlich, um eines oder mehreres des Folgenden zu versuchen:
1. Die Schuld für eine zu- oder abnehmende Zahl von irgendetwas einer Substanz, einer Maßnahme oder einer Gruppe in die Schuhe zu schieben, meistens fälschlich,
2. die Verwendung zweier derartiger Graphiken von Einzelzahlen, um irgendeine Einzelzahl mit irgendeiner anderen Einzelzahl zu korrelieren, um eine gewünschte Story zu verkaufen, gewöhnlich um etwas zu verurteilen oder zu begrüßen, meistens fälschlich,
3. Aufmerksamkeit (lies: öffentliche Besorgnis hervorzurufen) auf das Steigen oder Fallen einer Einzelzahl zu lenken in der Hoffnung, Fortschritte zu erzielen (hinsichtlich Forschungsgeldern, Ruhm, öffentlichem Wohlwollen, öffentliche oder politische Unterstützung), gewöhnlich nicht garantiert.
Diese Einzelzahlen, dazu erdacht, irgendwie einige Vorgänge in der realen Welt zu beleuchten, sind oftmals, vielleicht immer, keine realen Zahlen, die reale Dinge repräsentieren, sondern imaginäre Zahlen, die existierende Konzepte repräsentieren auf einem pragmatischen praktischen Niveau, nur in unseren Vorstellungen, welchen Bedeutung und Nützlichkeit fehlen könnte, oder beides. In dieser Speziellen Hinsicht könne wir diese Zahlen imaginäre Zahlen nennen. Und weil sie fast niemals als imaginäre Zahlen angesehen werden, welche besondere Sorgfalt hinsichtlich deren Anwendung erfordern, wird jeder einzelne der drei Punkte gefolgt von „gewöhnlich fälschlich“ oder „gewöhnlich nicht garantiert“.
Selbst wenn Sie mir nicht zustimmen, dürfte es interessant sein, in Kommentaren einige der fortgesetzten Bemühungen zu kommentieren, diese spezielle Art von abgeleiteten Zahlen zu (miss-)brauchen, die imaginäre Zahl, um die öffentliche Meinung auf differierenden wissenschaftlichen Gebieten zu beeinflussen.
———————————————
Schlussbemerkung des Autors: In diesem Beitrag geht es nicht wirklich um den globalen Meeresspiegel, aber ich bezweifle, dass wir über dieses Thema sprechen können, ohne gleichzeitig die Punkte zu berühren, die das Thema globaler mittlerer Meeresspiegel umgeben.
Lieber würde ich das Konzept von „Jagen wir imaginären Zahlen nach?“ diskutieren.
Nur mal so… reden wir darüber!
Link: http://wattsupwiththat.com/2015/10/09/are-we-chasing-imaginary-numbers/
Übersetzt von Chris Frey EIKE



Unsicherheits-Bandbreiten, Fehlerbalken und CIs

geschrieben von Kip Hansen | 12. Oktober 2016

Die NYTimes sowie tausende anderer Nachrichtenportale haben sowohl lautstark proklamiert, dass 2014 „das wärmste Jahr jemals“ gewesen ist, aber auch die Klagen gegen diese Proklamationen. Einige, wie der Opinion Blog der NYTimes Dot Earth haben unverhohlen beides abgedeckt.
Dr. David Whitehouse hat über die GWPF in seinem Beitrag bei WUWT hier widersprochen. Sein Beitrag trägt den Titel [übersetzt] „UK Met.-Office: 2014 war NICHT das wärmste Jahr jemals wegen der ,Unsicherheits-Bandbreiten‘ der Daten“:
„Der HadCRUT4-Datensatz (zusammengestellt vom Met.-Office und der CRU an der University of East Anglia) zeigt, dass die Temperatur des vorigen Jahres um 0,56°C (±0,1°C*) über dem langzeitlichen Mittel lag (1961 bis 1990). Nominell platziert dies das Jahr 2014 zusammen mit dem Jahr 2010 auf Rekordniveau, aber die Unsicherheits-Bandbreiten bedeuten, dass es nicht möglich ist definitiv zu sagen, welches der vielen letzten Jahre das Wärmste war“. Und unten auf der Seite: „*0,1°C ist die 95%-Unsicherheits-Bandbreite“.
Der Essay von David Whitehouse enthielt u. A. das folgende Bild: die jährlichen Mittel nach HadCRUT4 mit Balken, die die Unsicherheits-Bandbreite von ±0,1°C repräsentieren:

Das Journal Nature verfolgte lange Zeit eine Politik, die darauf bestand, dass Graphiken mit Fehlerbalken das beschreiben, was die Fehlerbalken repräsentieren. Ich dachte, dass dies in diesem Falle gut wäre, um genau zu sehen, was das Met.-Office mit „Unsicherheits-Bandbreite“ meint.
In den FAQ sagt das Met.-Office:
„Es ist unmöglich, die globale mittlere Temperaturanomalie mit perfekter Genauigkeit zu berechnen, weil die zugrunde liegenden Daten Messfehler enthalten und weil die Messungen nicht den gesamten Globus abdecken. Allerdings ist es möglich, die Genauigkeit zu quantifizieren, mit der wir die globale Temperatur messen können, und das ist ein wichtiger Bestandteil bei der Erstellung des HadCRUT4-Datensatzes. Die Genauigkeit, mit der wir die globale mittlere Temperatur des Jahres 2010 messen können, liegt bei rund einem Zehntel Grad Celsius. Die Differenz zwischen den mittleren Schätzungen für die Jahre 1998 und 2010 liegt bei etwa einem Hundertstel Grad Celsius, was weit unterhalb der Genauigkeit liegt, mit dem beide Werte jeweils berechnet werden können. Dies bedeutet, dass wir nicht sicher wissen können – jedenfalls allein aufgrund dieser Information – welches Jahr das Wärmere war. Allerdings beträgt die Differenz zwischen den Jahren 2010 und 1989 etwa 4 Zehntel Grad Celsius, so dass wir mit viel Vertrauen sagen können, dass das Jahr 2010 wärmer ausgefallen ist als das Jahr 1989 oder tatsächlich irgendein Jahr vor 1996“. (Hervorhebung von mir).
Ich applaudiere dem Met.-Office zu seiner Offenheit und klaren Sprache in diesem einfachen Statement.
Und jetzt zu der Frage, die sich aus dieser Abbildung ergibt:

Diese Graphik wurde aus Daten erstellt, die direkt vom UK Met.-Office stammen, „unberührt von menschlichen Händen“ (keine Zahlen wurden händisch kopiert, umgeschrieben, gerundet oder anderweitig modifiziert). Ich habe die CRUTEM4-Daten vom Festland allein grau dargestellt und sie gerade noch sichtbar zum Vergleich stehen gelassen. Links zu den öffentlich zugänglichen Datensätzen werden sie in der Graphik gezeigt. Ich habe einen Text und zwei graphische Elemente hinzugefügt:
a. In hellblau die Unsicherheitsbalken für den Wert 2014, rückwärtig ausgedehnt auf den gesamten Zeitraum,
b. Ein hellrosa Band, die Breite der Unsicherheit für diese Größe in der Graphik auf eine Weise überlagert, um deren Maximalwerte abzudecken.
Und jetzt die Frage:
Was bedeutet diese Illustration wissenschaftlich?
Genauer: Falls die Zahlen in Ihren Fachbereich fallen würden – Ingenieurswesen, Medizin, Geologie, Chemie, Statistik, Mathematik, Physik – und das Ergebnis längerer Messreihen wären, was würde es Ihnen bedeuten, dass:
a. 11 der 18 Mittelwerte des jüngsten Mittelwertes 2014 innerhalb der Unsicherheits-Balken liegen?
b. alle außer drei Werten (1996, 1999), 2000) überlagert werden können mit einem Band von der Breite der Unsicherheits-Bandbreite für die gemessene Größe?
Es wäre schön, wenn es Antworten gäbe aus so vielen Forschungsbereichen wie möglich.
———————————————————————————————–
Bemerkungen des Autors zu diesem Artikel: Ich habe keine Meinung bzgl. bestimmter Interessen hierzu – und auch keine besondere Erfahrung. (Oh, ich habe eine Meinung, aber die ist nicht gut fundiert). Mich würden Meinungen von Personen mit Forschungserfahrungen in anderen Bereichen interessieren.
Dies ist keine Diskussion der Frage „war 2014 das wärmste Jahr?“ oder irgendetwas dergleichen. Einfache Wiederholungen zu den Glaubensartikeln von beiden Seiten der Globale-Erwärmungs-Kirche würden nichts Wesentliches zu dieser Diskussion beitragen und sollten anderswo gepostet werden.
Um mit Judith Curry zu sprechen: Dies ist ein technischer Beitrag – dazu gedacht, eine Diskussion zu erhalten über wissenschaftliche Methoden zur Erkennung dessen, was Unsicherheits-Bandbreiten, Fehlerbalken und CIs uns über die Forschungsergebnisse verraten können und verraten. Bitte die Kommentare auf diesen Bereich beschränken; vielen Dank.
Soweit dieser Artikel. Auf Bitte von Herrn Limburg werden hierzu abweichend von der üblichen Praxis auch noch ein paar Kommentare übersetzt. Fachlich berühren diese mich nur peripher, aber sie zeigen, wie man sachlich, konstruktiv und trotzdem kontrovers diskutieren kann. Die Hyperlinks hinter den Bezeichnungen der Kommentatoren wurden entfernt. – Anm. d. Übers.
Einige Kommentare zu diesem Artikel:
oz4caster
Ich glaube, dass sie zu vertrauensselig sind hinsichtlich einer Genauigkeit von 0,1°C für jüngste globale Temperaturanomalien. Mein Tipp wären mindestens 0,2°C bis 0,3°C bis zu 0,5°C während der letzten Jahre und möglicherweise bis zu 1,0°C in früheren Jahren in dem Datensatz. Ich habe den Verdacht, dass die größten Unsicherheitsquellen die sehr geringe räumliche Abdeckung, Repräsentativität der Messungen, Veränderungen der Messorte und „Homogenisierung“ sind, die die Unsicherheit eher vergrößern anstatt sie zu verringern. Der genaue Aufstellungsort ist kritisch für repräsentative Messungen, und das USCRN hilft, dieses Problem anzugehen, allerdings nur für einen sehr kleinen Teil des Globus‘.
Erwiderung hierzu:
george e. smith
Aus dem Artikel: „Der HadCRUT4-Datensatz (zusammengestellt vom Met.-Office und der CRU an der University of East Anglia) zeigt, dass die Temperatur des vorigen Jahres um 0,56°C (±0,1°C*) über dem langzeitlichen Mittel lag (1961 bis 1990)“
Nun, mit dieser Feststellung habe ich einige Probleme.
Zunächst: die Bezugsperiode 1961 bis 1990. Dies schließt bequemerweise jene Periode in den siebziger Jahren ein, als man die Klimakrise in Gestalt einer bevorstehenden Eiszeit kolportiert hat, zusammen mit abenteuerlichen Vorschlägen, Ruß auf dem arktischen Eis zu verstreuen, um die vermeintliche Eiszeit abzuwehren. Globale Hungersnöte wurden von genau der gleichen Bande von Kontrollfreaks vorhergesagt, die jetzt versucht, das globale Überkochen zu verhindern.
Außerdem liegt die Hälfte dieser Bezugsperiode vor der Satellitenära, die, glaube ich, etwa um das Jahr 1979 begann, was fast genau zusammenfällt mit der Ausbringung der ersten ozeanischen Messbojen, die in der Lage waren, simultan Messungen der Wassertemperatur an der Oberfläche (bis zu 1 m Tiefe) sowie Lufttemperaturen über der Oberfläche (bis zu 3 m) durchzuführen. 2001 zeigten diese Bojendaten (über etwa 20 Jahre), dass Wasser- und Lufttemperaturen nicht gleich und auch nicht korreliert waren. Warum sollte irgendjemand sich auch nur vorstellen, dass beides doch der Fall war?
Fazit: Ich glaube keinen „globalen“ Klimatemperaturen vor dem Jahr 1980. Und warum hört man mit dem Vergleich 25 Jahre vor heute auf?
Warum verwendet man nicht das Mittel ALLER glaubwürdigen Daten, die man hat? Anderenfalls wären die Zahlen der Bezugsperiode reine Rosinenpickerei.
Man verleihe also den HadCRUT-Daten vor 1980 keinerlei Glaubwürdigkeit oder irgendwelchen anderen Angaben, die man später aus diesen nutzlosen frühen Daten ableiten könnte.
Und schließlich glaube ich nicht, dass irgendeine Strategie bzgl. Stichproben legitim sind, steht dies doch im Gegensatz zur Theorie von Stichproben (man wäre nicht in der Lage, dies zu lesen, falls das nicht der Fall wäre).
Epiphron Elpis
Erwiderung hierauf:
Die Schlussfolgerungen sind unabhängig von der Bezugsperiode. Und irgendeine andere gewählte Bezugsperiode würde die gleichen Trends und die gleichen Temperaturdifferenzen zeigen.
Kip Hansen
Antwort an oz4caster: Ich denke, dass die Unsicherheits-Bandbreite von 0,1°C zu klein ist selbst für Messungen aus jüngster Zeit. Aber für diese Diskussion lasse ich das mal so durchgehen – es ist fast ein Wunder, dass sie eine solche Unsicherheits-Bandbreite überhaupt zugeben.
Ich arbeite langfristig an einem Beitrag, der aktuelle Original-Messfehler erkundet bei der Temperatur der Welt mit der Zeit, und was dies für die globalen Mittelwerte bedeutet.
Zum Beispiel weiß ich, dass die ,krigging‘ [wie übersetzt man dieses Adjektiv?] Ergebnisse von BEST nur maximal zu 0,49°C akkurat sind.
davidmhoffer
Das Erste, was ich bei einer solchen Graphik fragen würde ist, ob das berechnete Mittel überhaupt relevant ist. Da die Temperatur nicht linear mit Strahlung (W/m²) variiert, ist es möglich, unterschiedliche räumliche Temperaturverteilungen zu erhalten, die zwar identische Mittelwerte aufweisen, aber sehr unterschiedliche Energiebilanzen. Beispiel: Zwei Punkte mit einer Temperatur von 280 K bzw. 320 K würden einen Mittelwert von 300 K zeigen und ein Strahlungsgleichgewicht von 471,5 W/m². Aber zwei Punkte mit einer Temperatur von 300 K an beiden Stellen würden ebenfalls einen Mittelwert von 300 K, jedoch ein Strahlungsgleichgewicht von 459,3 W/m² aufweisen.
Damit im Hinterkopf lassen die Fehlerbalken nicht nur keine Schlussfolgerung hinsichtlich des Temperaturtrends zu, d. h. ob er positiv oder nicht bedeutungslos ist, sondern die Fehlerbreite der Gleichgewichts-Energiebilanz ist wegen der nichtlinearen Beziehung zwischen beiden viel größer. Da AGW auf der Prämisse basiert, dass zunehmendes CO2 die Energiebilanz der Erde ändert, ist der Versuch, die Art und Weise zu quantifizieren, mit der es das tut, die Mittelung eines Parameters, der keine direkte Beziehung zur Energiebilanz hat. Damit bleibt die Graphik zurück als selbst bedeutungslos hinsichtlich statistischer Genauigkeit und auch der Physik.
Antwort darauf:
Steven Mosher
Zitat: „Das Erste, was ich bei einer solchen Graphik fragen würde ist, ob das berechnete Mittel überhaupt relevant ist“.
Tatsächlich ist sie überhaupt kein Mittelwert von Temperaturen.
Obwohl die meisten Menschen, die der Klimadiskussion folgen, dies nicht verstehen (tatsächlich verstehen die Meisten, die solche Mittelwerte erstellen, das selbst nicht).
Was ist das globale Temperaturmittel wert, wenn es nicht wirklich ein Mittel ist.
Mathematisch handelt es sich um eine Vorhersage. Es ist eine Vorhersage dessen, was man an instrumentenfreien Standorten messen würde.
„Stationsbeobachtungen werden allgemein verwendet, um Klimavariablen auf Gitternetzen vorherzusagen (predict), wobei der statistische Terminus „Vorhersage“ (prediction) hier benutzt wird als „räumliche Interpolation“ oder „räumlich-zeitliche Interpolation“. Er sollte nicht mit „forecasting“ verwechselt werden*. Gründliche Begutachtungen von in Meteorologie und Klimatologie verwendeten Interpolationsverfahren wurden jüngst von Price et al. (2000), Jarvis und Stuart (2001), Tveito et al. (2006) und Stahl et al. (2006) vorgelegt. Die Literatur zeigt, dass die am meisten verwendeten Interpolationsverfahren in Meteorologie und Klimatologie folgende sind: Verfahren größter Nachbarschaft, Splines [?], Regression und Kriging [?]; aber auch neurale Netzwerke und Machine learning techniques [?].
[*Ich glaube zwar, mich in der englischen Sprache ganz gut auszukennen, aber der hier angesprochene Bedeutungsunterschied zwischen den Wörtern „prediction“ und „forecast“ ist mir unbekannt. Vielleicht weiß jemand Näheres? Auch die am Ende dieses Absatzes stehenden und mit einem Fragezeichen versehenen Fachbegriffe sind mir unbekannt. Anm. d. Übers.]
Aus: Räumlich-zeitliche Interpolation täglicher Temperaturwerte für globale Landgebiete mit einer Auflösung von 1 km. – Autoren: Milan Kilibarda1,*, Tomislav Hengl2, Gerard B. M. Heuvelink3, Benedikt Gräler4, Edzer Pebesma4, Melita Perčec Tadić5 and Branislav Bajat1.
Wenn man also liest, dass das globale Mittel für Dezember 2014 15,34°C beträgt, bedeutet das Folgendes:
Wenn man mit einem perfekten Thermometer an zufälligen Stellen des Globus‘ misst, wird eine Schätzung von 15,34°C den Fehler minimieren.
Wählt man 1000 zufällige Stellen ohne Thermometer aus, minimiert eine Vorhersage (prediction) den Fehler.
Antwort hierzu:
Danny Thomas
Steven,
danke für jene Beschreibung. Um mit BEST so fair wie möglich zu sein – es scheint, als bieten sie mit einiger Sicherheit eine vernünftige Evaluierung ihrer Analyse für 2014 an als eines der fünf wärmsten Jahre. Kip Hansen sagte, dass wir auf der Diskussion der „Unsicherheits-Bandbreiten“ bestehen. Um dies so weit wie möglich zu achten, wären Sie willens zu diskutieren, wie die Entscheidung gefallen ist, das Arbeitsergebnis zu titulieren mit „Die Mittlere Temperatur 2014 von Berkeley Earth“, wenn in Wirklichkeit diese Arbeit prädiktiver Natur ist und nicht das enthält, was der Titel nahelegt? Mit anderen Worten, warum lautet der Titel nicht „das prädiktive Mittel…“ (hier).
MET scheint eine vernünftigere Beschreibung ihrer Arbeit und des Vertrauensniveaus abzugeben. NOAA und NASA aber nicht so sehr, wenn selbst die oberflächlichste Sicht auf ihr Vertrauensniveau entweder zu einem klaren Plan der Irreführung führt im Vergleich zu ihren Schlagzeilen oder zur Befürwortung von AGW-Propaganda trotz fehlender guter wissenschaftlicher Kommentare.
bones
Vor der neuen Mathematik war es gewöhnlich der Fall, dass das arithmetische Mittel auch die Kleinste-Quadrate-Best-Estimate war, welche zufällig verteilte Fehler minimieren würde. Man kann glauben, dass Verfahren unter Verwendung von Kriging, neuralen Netzwerken und machine learning techniques ein Ergebnis zeitigen, das Fehler minimiert, aber man erwarte nicht, dass ich diesen Mist glaube.
davidmhoffer
Zitat: „Tatsächlich ist sie überhaupt kein Mittelwert von Temperaturen.
Obwohl die meisten Menschen, die der Klimadiskussion folgen, dies nicht verstehen (tatsächlich verstehen die Meisten, die solche Mittelwerte erstellen, das selbst nicht).“
Ich verstehe Ihren Punkt und stimme dem auch bis zu einem gewissen Grad zu, obwohl Ihre Vermutung amüsant finde, dass selbst die die Berechnungen durchführenden Menschen nicht verstehen, was das ist. Damit ändert Ihr Standpunkt aber nicht meinen. Mein Punkt ist nicht, wie man einen Mittelwert für einen bestimmten Punkt mit der Zeit berechnet, sondern was die Änderung in jenem Mittelwert impliziert. Man nenne es ein Mittel, man nenne es eine Vorhersage (prediction) einer zufälligen Messung – da jene Messung sich mit der Zeit ändert infolge der nichtlinearen Beziehung zwischen Temperatur und Strahlung, ist die berechnete Änderung sogar noch bedeutungsloser als die Fehlerbalken suggerieren. Die Änderung des Wertes kann nicht die Änderung der Energiebilanz repräsentieren, weil einfache Physik vorschreibt, dass kalte Temperatur-Regimes (Nacht, Winter, hohe Breiten, große Höhe) überrepräsentiert und warme Temperatur-Regimes (Tag, Sommer, niedrige Breiten, geringe Höhe) unterrepräsentiert sind.
Der Rohwert der von Ihnen illustrierten Vorhersage (prediction) ist das Eine; die Änderung jenes Wertes aber etwas Anderes. Jene Änderung hat keine direkte Beziehung zu der interessierenden Metrik (Änderung des Energie-Gleichgewichtes), egal wie Sie es definieren.
Walt D.
Nehmen wir einmal die Antarktis als ein Gebiet mit sehr wenigen Daten. Sie behaupten, dass eine mittlere Temperatur von 15,34°C den Schätzfehler minimiert. Höchst unwahrscheinlich besonders im antarktischen Winter. Es ist absurd zu zeigen, dass die Temperaturen am Südpol und im Death Valley als zufällige Werte angesehen werden können, gewonnen aus der gleichen Verteilung mit dem gleichen Mittel und den gleichen Varianzen. Darum arbeiten die Menschen mit Änderungen der Temperatur und nicht mit den tatsächlichen Temperaturen selbst.
Jeff F
@bones: Tatsache ist, dass die Verwendung von Daten, die mit den zuvor erwähnten Verfahren eingehen, nicht wirklich neue Mathematik ist. Die Verfahren wurden schon geraume Zeit angewendet. Allerdings ist das Problem hier, dass viele Leute diese anwenden, ohne deren Implikationen zu verstehen. Mit vielen dieser Verfahren KANN NICHT gezeigt werden, dass sie Fehler minimieren – außer unter ganz besonderen Umständen. Zum Beispiel ist Kriging nur eine unverzerrte Schätzfunktion, falls der Prozess stationär ist. Schlimmer noch ist, dass es wirklich keine Rechtfertigung dafür gibt, Klimadaten überhaupt als einen stochastischen Prozess zu behandeln.
In anderen Disziplinen, wo wir diese Verfahren für die Datenanalyse anwenden, zeigen wir Beispiele, wo sie funktioniert haben, und überlassen es dem User zu entscheiden, ob die Verfahren für sein Problem geeignet sind. Aber wir stellen KEINE Behauptungen auf über die Optimalität des Verfahrens. Weil wir wissen, dass wir das nicht können. Allerdings habe ich VIEL zu viele klimawissenschaftliche Studien gelesen, die weiter entwickelte Verfahren allein zu dem Zweck angewendet haben, um eine Behauptung über den zugrunde liegenden PROZESS zu rechtfertigen, der die Daten erzeugt hat! Falls wenige Behauptungen über die statistischen Charakteristika der DATEN selbst erhoben werden können, wenn man diese Verfahren anwendet, kann man fast nichts über den PROZESS aus diesen Daten aussagen.
IvanV
@ Steven Mosher & davidmhoffer
Ich versuche gerade, Ihre Punkte nachzuvollziehen und die Unterschiede zwischen ihnen.
Steven Mosher, was Sie sagen, ähnelt einem Fall, wo man zwei Stationen in den Tropen hat mit einem Mittel von 30°C und eine nahe den Polen mit einem Mittel von 0°C. Dann würde die Best Estimate der globalen mittleren Temperatur 15°C betragen, da dies den Fehler zwischen den Messungen minimieren würde?
Davidmhoffer, aus Sicht des Energiegleichgewichtes wäre die Best Estimate der globalen Mitteltemperatur die Temperatur einer Sphäre mit gleichmäßiger Temperatur, die das gleiche Energie-Gesamtgleichgewicht aufweist?
ferdberple
Mathematisch ist es eine Vorhersage (prediction). Es ist eine Vorhersage dessen, was man an nicht mit Instrumenten ausgestatteten Stellen messen würde.
Auf dieser Grundlage wird die Stichproben-Theorie einen realistischeren Wert ergeben als die gegenwärtige Praxis, Stationen zu adjustieren, damit sie statisch aussehen.
Nehmen wir einfach mal an, dass jede Stationsablesung einmalig ist. Dass die Station selbst verlagert werden kann oder anderweitig von einer Messung zur nächsten verändert wird, und dass jeder Versuch von Adjustierungen, um eine kontinuierliche Stationsaufzeichnung zu erhalten einfach noch mehr unbekannte Fehler einführen wird.
Es gibt keine Notwendigkeit. Da man den Wert an unbekannten Punkten vorhersagt (predict), wird eine Stichprobe an bekannten Punkten ausreichen, während die Möglichkeit eingeführter Fehler eliminiert wird. Alles, was erforderlich ist, ist ein Stichproben-Algorithmus, der zu der räumlichen und zeitlichen Verteilung der Erdoberfläche passt.
Und so weiter. Es gibt über 300 weitere Kommentare zu dem Artikel. Als Grundlage für das hier besprochene Problem soll die Übersetzung bis hier aber erst einmal reichen.
Link: http://wattsupwiththat.com/2015/02/01/uncertainty-ranges-error-bars-and-cis/
Übersetzt von Chris Frey EIKE